题目内容
20.若f(x)=loga(2+x)在区间(-2,+∞)是单调递减函数,则a的取值范围是( )| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (1,+∞) |
分析 根据复合函数单调性“同增异减”的原则,结合已知中f(x)=loga(2+x)在区间(-2,+∞)是单调递减函数,可得a的取值范围.
解答 解:∵f(x)=loga(2+x)在区间(-2,+∞)是单调递减函数,
t=2+x在区间(-2,+∞)是单调递增函数,
∴y=logat为减函数,
故a∈(0,1),
故选:A
点评 本题考查的知识点是复合函数的单调性,熟练掌握复合函数单调性“同增异减”的原则,是解答的关键.

练习册系列答案
相关题目
8. 如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S为( )(注:圆台侧面积公式为S=π(R+r)l)
如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S为( )(注:圆台侧面积公式为S=π(R+r)l)
 如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S为( )(注:圆台侧面积公式为S=π(R+r)l)
如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S为( )(注:圆台侧面积公式为S=π(R+r)l)| A. | 17π+3$\sqrt{17}$π | B. | 20π+5$\sqrt{17}$π | C. | 22π | D. | 17π+5$\sqrt{17}$π |
9.在原命题及其逆命题、否命题、逆否命题中,真命题的个数可以是( )
| A. | 1或2或3或4 | B. | 0或2或4 | C. | 1或3 | D. | 0 |
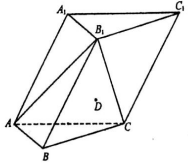 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.