题目内容
(12分)设函数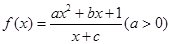 为奇函数,且
为奇函数,且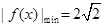 ,数列
,数列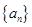 与
与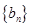 满足如下关系:
满足如下关系: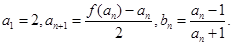
(1)求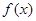 的解析式;
的解析式;
(2)求数列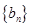 的通项公式
的通项公式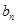 ;
;
(3)记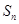 为数列
为数列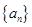 的前
的前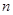 项和,求证:对任意的
项和,求证:对任意的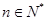 有
有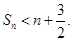
【答案】
略.
【解析】(1)先根据 恒成立,可求出b=c=0,再根据|f(x)|的最小值可求出a=2.从而确定
恒成立,可求出b=c=0,再根据|f(x)|的最小值可求出a=2.从而确定 .
.
(2)根据 ,可得到
,可得到 ,
,
两边取常用对数可得 ,
,
所以{ }为等比数列.从而得到其通项,进而得到
}为等比数列.从而得到其通项,进而得到 的通项公式.
的通项公式.
(3)在(2)的基础上,由bn可求出an,然后考虑采用不等式放缩和二项式定理来解决,难度大,综合性强,必须基本功扎实.

练习册系列答案
相关题目
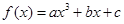
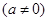 为奇函数,其图象在点
为奇函数,其图象在点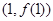 处的切线与直线
处的切线与直线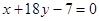 垂直,导函数
垂直,导函数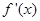 的最小值为
的最小值为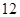 .
.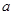 ,
,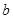 ,
,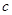 的值;
的值;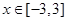 时,
时,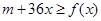 恒成立,求
恒成立,求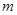 的范围;
的范围;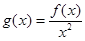 ,当
,当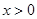 时,求
时,求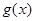 的最小值.
的最小值.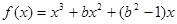 为奇函数,函数
为奇函数,函数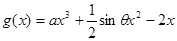 在区间
在区间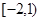 上单调递减,在
上单调递减,在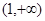 上单调递增.
上单调递增.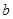 的值;
的值;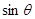 的值及
的值及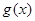 的解析式;
的解析式;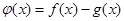 ,试证:对任意的
,试证:对任意的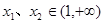 且
且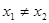 都有
都有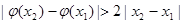 .
.