题目内容
(本题满分12分)设函数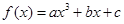
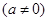 为奇函数,其图象在点
为奇函数,其图象在点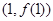 处的切线与直线
处的切线与直线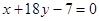 垂直,导函数
垂直,导函数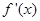 的最小值为
的最小值为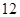 .
.
(1)求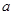 ,
,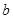 ,
,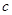 的值;
的值;
(2)若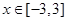 时,
时,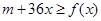 恒成立,求
恒成立,求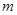 的范围;
的范围;
(3)设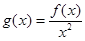 ,当
,当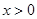 时,求
时,求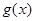 的最小值.
的最小值.
【答案】
(1) ,
, ,
,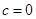 (2)
(2)  (3)
(3)
【解析】
(1)∵ 为奇函数,∴
为奇函数,∴ ,即
,即 ,
,
∴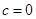 ,又∵
,又∵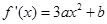 的最小值为
的最小值为 ,∴
,∴ ;
;
又直线 的斜率为
的斜率为 ,因此,
,因此, ,
∴
,
∴ ,
,
∴ ,
, ,
,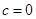 为所求.
为所求.
(2)  在
在 上的最大是32,
上的最大是32,
(3)由(1)得 ,∴当
,∴当 时,
时,
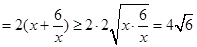 ,
,
∴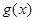 的最小值为
的最小值为 .
.
思路分析:(1)∵ 为奇函数,∴
为奇函数,∴ ,即
,即 ,
,
∴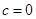 ,∵
,∵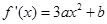 的最小值为
的最小值为 ,∴
,∴ ;由题意得
;由题意得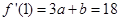
 ;
;
(2) 时,
时, 恒成立,即
恒成立,即 恒成立,构造函数
恒成立,构造函数 ,求其在
,求其在 上的最大值;
上的最大值;
(3)由(1)得 ,当
,当 时,
时,
 根据基本不等式求得最小值为
根据基本不等式求得最小值为 .
.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;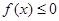 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求