题目内容
 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2| 2 |
(1)求证:BD⊥平面PAC;
(2)求异面直AC与PD所成角的余弦值;
(3)设Q为线段PB上一点,且直线QC与平面PAC所成角的正弦值为
| ||
| 3 |
| PQ |
| PB |
考点:直线与平面所成的角,异面直线及其所成的角,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系,由此利用向量法能证明BD⊥平面PAC.
(2)由
=(2,2
,0),
=(0,-2
,4),利用向量法能求出异成直线AC与PD所成角的余弦值.
(3)设
=λ(其中0<λ<1),Q(x,y,z),设直线QC与平面PAC所成角为θ.利用向量法能求出
的值.
(2)由
| AC |
| 2 |
| DP |
| 2 |
(3)设
| PQ |
| PB |
| PQ |
| PB |
解答:
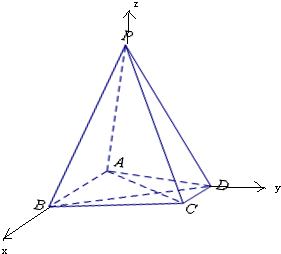 (1)证明:∵PA⊥平面ABCD,AB⊥AD,
(1)证明:∵PA⊥平面ABCD,AB⊥AD,
∴以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴,
建立空间直角坐标系,…(1分)
则B(4,0,0),P(0,0,4),D(0,2
,0),C(2,2
,0).
∴
=(-4,2
,0),
=(2,2
,0),
=(0,0,4),…(2分)
∴
•
=(-4)×2+2
×2
+0×0=0,
•
=(-4)×0+2
×0+0×4=0.
∴BD⊥AC,BD⊥AP.
∵AP∩AC=A,AC?平面PAC,PA?平面PAC,
∴BD⊥平面PAC.…(4分)
(2)解:∵
=(2,2
,0),
=(0,-2
,4)…(5分)cos<
,
>=-
,
∴异成直线AC与PD所成角的余弦值
…(8分)
(3)解:设
=λ(其中0<λ<1),Q(x,y,z),
设直线QC与平面PAC所成角为θ.
∴
=λ
,∴(x,y,z-4)=λ(4,0,-4).
∴
即Q(4λ,0,-4λ+4).…(9分)
∴
=(4λ-2,-2
,-4λ+4).
平面PAC的一个法向量为
=(-4,2
,0).…(10分)
∵sinθ=|cos<
,
>|=|
|,
∴
=|
|.…(11分)
解得λ=
∈[0,1].
∴
=
.…(12分)
 (1)证明:∵PA⊥平面ABCD,AB⊥AD,
(1)证明:∵PA⊥平面ABCD,AB⊥AD,∴以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴,
建立空间直角坐标系,…(1分)
则B(4,0,0),P(0,0,4),D(0,2
| 2 |
| 2 |
∴
| BD |
| 2 |
| AC |
| 2 |
| AP |
∴
| BD |
| AC |
| 2 |
| 2 |
| BD |
| AP |
| 2 |
∴BD⊥AC,BD⊥AP.
∵AP∩AC=A,AC?平面PAC,PA?平面PAC,
∴BD⊥平面PAC.…(4分)
(2)解:∵
| AC |
| 2 |
| DP |
| 2 |
| AC |
| DP |
| ||
| 3 |
∴异成直线AC与PD所成角的余弦值
| ||
| 3 |
(3)解:设
| PQ |
| PB |
设直线QC与平面PAC所成角为θ.
∴
| PQ |
| PB |
∴
|
∴
| CQ |
| 2 |
平面PAC的一个法向量为
| BD |
| 2 |
∵sinθ=|cos<
| CQ |
| BD |
| ||||
|
|
∴
| ||
| 3 |
| -4(4λ-2)-8 | ||||
2
|
解得λ=
| 7 |
| 12 |
∴
| PQ |
| PB |
| 7 |
| 12 |
点评:本题考查直线与平面垂直的证明,考查异面直线所成角的余弦值的求法,考查两线段比值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知集合A={x∈R|x2≤4},B={x∈N|
≤3},则A∩B的非空子集的个数( )
| x |
| A、3 | B、4 | C、7 | D、8 |