题目内容
13.已知(1+ax)5(1-2x)4的展开式中x2的系数为-16,则实数a的值为2.分析 由于(1+ax)5(1-2x)4=$(1+{∁}_{5}^{1}ax+{∁}_{5}^{2}{a}^{2}{x}^{2}+…)$$(1-{∁}_{4}^{1}×2x+{∁}_{4}^{2}×4{x}^{2}+…)$,即可得出.
解答 解:(1+ax)5(1-2x)4=$(1+{∁}_{5}^{1}ax+{∁}_{5}^{2}{a}^{2}{x}^{2}+…)$$(1-{∁}_{4}^{1}×2x+{∁}_{4}^{2}×4{x}^{2}+…)$,
由于展开式中x2的系数为-16,则${∁}_{4}^{2}$×4+$-2{∁}_{4}^{1}$×${∁}_{5}^{1}a$+${∁}_{5}^{2}{a}^{2}$=-16,
化为:a2-4a+4=0,
解得a=2.
故答案为:2.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.若集合A={x|x2-2x-3>0},集合B={x|3x>8},则A∩B等于( )
| A. | (-1,3) | B. | (-∞,-1) | C. | (3,+∞) | D. | (log38,+∞) |
8.计算sin47°cos17°+cos47°cos107°的结果等于( )
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
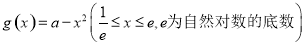 与
与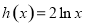 的图象上存在关于
的图象上存在关于 轴对称的点,则实数
轴对称的点,则实数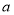 的取值范围是( )
的取值范围是( )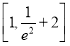 B.
B.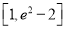 C.
C.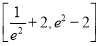 D.
D.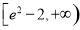

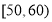 的频率及全班人数;
的频率及全班人数;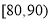 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中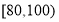 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在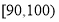 之间的概率.
之间的概率.
 如图,已知椭圆Ⅰ与椭圆Ⅱ有公共左顶点A与公共左焦点F,且椭圆Ⅰ的长轴长是椭圆Ⅱ的长釉长的k(k>1,且k为常数)倍,则椭圆Ⅰ的离心率的取值范围是$(1-\frac{1}{k},1)$.
如图,已知椭圆Ⅰ与椭圆Ⅱ有公共左顶点A与公共左焦点F,且椭圆Ⅰ的长轴长是椭圆Ⅱ的长釉长的k(k>1,且k为常数)倍,则椭圆Ⅰ的离心率的取值范围是$(1-\frac{1}{k},1)$.