题目内容
15.已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)≥$\frac{1}{2}$,则f(x)<$\frac{x}{2}$+$\frac{1}{2}$的解集为( )| A. | {x|x<1} | B. | {x|x>1} | C. | {x|x<-1} | D. | {x|x>-1} |
分析 根据条件构造函数g(x)=f(x)-$\frac{x}{2}$-$\frac{1}{2}$,然后利用导数研究函数的单调性和最值即可得到结论.
解答 解:设g(x)=f(x)-$\frac{x}{2}$-$\frac{1}{2}$,
则g'(x)=f'(x)-$\frac{1}{2}$,
∵f(x)的导函数f′(x)≥$\frac{1}{2}$,
∴g'(x))=f'(x)-$\frac{1}{2}≥$0,
即函数g(x)在定义域上单调递增,
∵g(1)=f(1)-$\frac{1}{2}-$$\frac{1}{2}$=0,
∴当x<1时,g(x)<g(1)=0,
∴不等式f(x)<$\frac{x}{2}$+$\frac{1}{2}$的解集为(-∞,1),
故选:A.
点评 本题主要考查不等式的解法,利用条件构造函数,利用导数研究函数的单调性是解决本题的关键,综合考查函数的性质.

练习册系列答案
相关题目
3.已知函数f(x)=x(2lnx-ax)有两个极值点,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (0,+∞) |
4.曲线y=$\frac{1}{x}$与y=x2在它们交点处的两条切线与x轴所围成的三角形的面积为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{3}{8}$ |
5.为迎接2013年全运会的到来,组委会在大连市招募了100名志愿者,其中男、女志愿者各50名,调查是否喜欢运动得到如下统计数据.由于一些原因,丢失了其中四个数据,目前知道这四个数据c,a,b,d恰好成递增的等差数列.
(Ⅰ)将联表中数据补充完整,并判断是否有95%的把握认为性别与运动有关?
(Ⅱ) 调查中显示喜欢运动的男志愿者中有10%懂得医疗救护,而喜欢运动的女志愿者中有40%懂得医疗救护,从中抽取2人组成医疗救护小组,则这个医疗救护小组恰好是一男一女的概率有多大?
附:χ2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜欢运动 | 不喜欢运动 | 总计 | |
| 男 | a | b | 50 |
| 女 | c | d | 50 |
| 总计 | 30 | 70 | 100 |
(Ⅱ) 调查中显示喜欢运动的男志愿者中有10%懂得医疗救护,而喜欢运动的女志愿者中有40%懂得医疗救护,从中抽取2人组成医疗救护小组,则这个医疗救护小组恰好是一男一女的概率有多大?
附:χ2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(χ2≥k) | 0.05 | 0.001 |
| k | 3.841 | 6.635 |
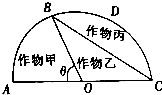 某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.
某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.