题目内容
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证:BD∥平面EFGH;
(2)求证:四边形EFGH是矩形.
(1)求证:BD∥平面EFGH;
(2)求证:四边形EFGH是矩形.

证明:(1)∵E,H分别为AB,DA的中点,
∴EH∥BD,又BD?平面EFGH,EH?平面EFGH,
∴BD∥平面EFGH.…(4分)
(2)取BD中点O,连续OA,OC,∵AB=AD,BC=DC.∴AO⊥BD,CO⊥BD.
又AO∩CO=0.∴BD⊥平面AOC,∴BD⊥AC. …(7分)
∵E,F,G,H为AB,BC,CD,DA的中点.
∴EH∥BD,且EH=
BD;FG∥BD,且FG=
BD,EF∥AC.
∴EH∥FG,且EH=FG,∴四边形EFGH是平行四边形.…(10分)
由AC⊥BD、EF∥AC、EH∥BD,∴EF⊥EH,∴四边形EFGH为矩形. …(12分)
∴EH∥BD,又BD?平面EFGH,EH?平面EFGH,
∴BD∥平面EFGH.…(4分)
(2)取BD中点O,连续OA,OC,∵AB=AD,BC=DC.∴AO⊥BD,CO⊥BD.
又AO∩CO=0.∴BD⊥平面AOC,∴BD⊥AC. …(7分)
∵E,F,G,H为AB,BC,CD,DA的中点.
∴EH∥BD,且EH=
| 1 |
| 2 |
| 1 |
| 2 |
∴EH∥FG,且EH=FG,∴四边形EFGH是平行四边形.…(10分)
由AC⊥BD、EF∥AC、EH∥BD,∴EF⊥EH,∴四边形EFGH为矩形. …(12分)

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
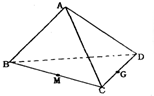 如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则
如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H. 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且
如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且 如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2
如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2