题目内容
(本小题满分14分)给定函数
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足, 求证:
求证: ;
;
(3)设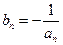 ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。

(1)试求函数
 的单调减区间;
的单调减区间;(2)已知各项均为负的数列
 满足,
满足, 求证:
求证: ;
;(3)设
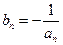 ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。(1)  的定义域为
的定义域为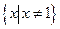 ………1分 (此处不写定义域,结果正确不扣分)
………1分 (此处不写定义域,结果正确不扣分)
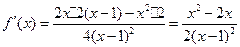 …………3分
…………3分
由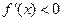 得
得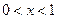 或
或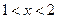
单调减区间为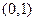 和
和 ………5分(答案写成(0,2)扣1分;不写区间形式扣1分)
………5分(答案写成(0,2)扣1分;不写区间形式扣1分)
(2)由已知可得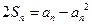 , 当
, 当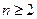 时,
时,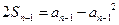
两式相减得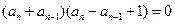
∴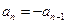 或
或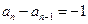
当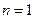 时,
时,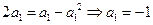 ,若
,若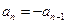 ,则
,则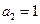 这与题设矛盾
这与题设矛盾
∴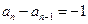 ∴
∴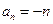 ……8分
……8分
于是,待证不等式即为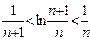 。
。
为此,我们考虑证明不等式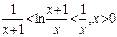
令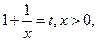 则
则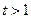 ,
,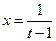
再令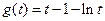 ,
,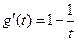 由
由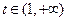 知
知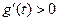
∴当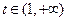 时,
时,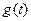 单调递增 ∴
单调递增 ∴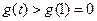 于是
于是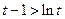
即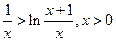 ①
①
令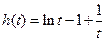 ,
,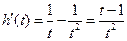 由
由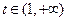 知
知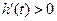
∴当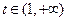 时,
时,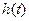 单调递增 ∴
单调递增 ∴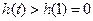
 于是
于是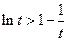
即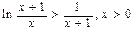 ②
②
由①、②可知 ………………10分
………………10分
所以,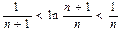 ,即
,即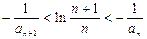 ………………11分
………………11分
(3)由(2)可知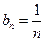 则
则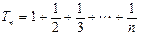 ……12分
……12分
在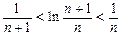 中令n=1,2,3…………..2010,2011并将各式相加得
中令n=1,2,3…………..2010,2011并将各式相加得
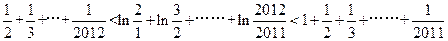 ……13分
……13分
即 ………………14分
………………14分
 的定义域为
的定义域为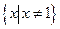 ………1分 (此处不写定义域,结果正确不扣分)
………1分 (此处不写定义域,结果正确不扣分) 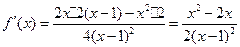 …………3分
…………3分 由
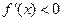 得
得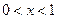 或
或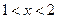
单调减区间为
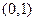 和
和 ………5分(答案写成(0,2)扣1分;不写区间形式扣1分)
………5分(答案写成(0,2)扣1分;不写区间形式扣1分)(2)由已知可得
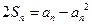 , 当
, 当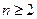 时,
时,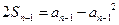
两式相减得
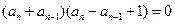
∴
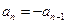 或
或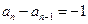
当
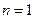 时,
时,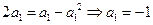 ,若
,若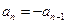 ,则
,则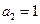 这与题设矛盾
这与题设矛盾∴
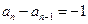 ∴
∴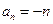 ……8分
……8分于是,待证不等式即为
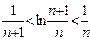 。
。为此,我们考虑证明不等式
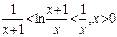
令
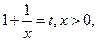 则
则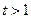 ,
,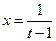
再令
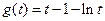 ,
,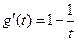 由
由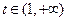 知
知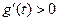
∴当
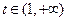 时,
时,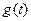 单调递增 ∴
单调递增 ∴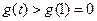 于是
于是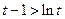
即
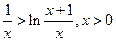 ①
①令
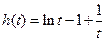 ,
,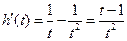 由
由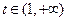 知
知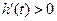
∴当
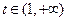 时,
时,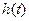 单调递增 ∴
单调递增 ∴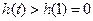
 于是
于是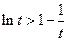
即
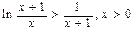 ②
②由①、②可知
 ………………10分
………………10分所以,
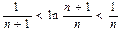 ,即
,即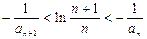 ………………11分
………………11分(3)由(2)可知
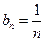 则
则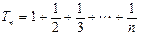 ……12分
……12分在
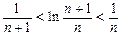 中令n=1,2,3…………..2010,2011并将各式相加得
中令n=1,2,3…………..2010,2011并将各式相加得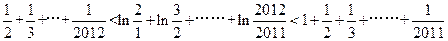 ……13分
……13分即
 ………………14分
………………14分略

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 上的函数
上的函数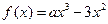 ,其中
,其中 为大于零的常数.
为大于零的常数.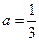 时,令
时,令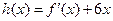 ,
, 时,
时, (
( 为自然对数的底数);
为自然对数的底数); ,在
,在 处取得最大值,
处取得最大值, (
(
 在定义域上为单调增函数,求
在定义域上为单调增函数,求 的取值范围;
的取值范围;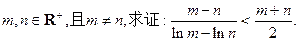
 ,
, ,
,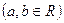
 时,若
时,若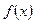 在
在 上单调递增,求
上单调递增,求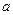 的取值范围;
的取值范围; :当
:当 ,使得
,使得 是
是 是
是 的最小值;
的最小值;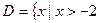 ,且
,且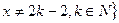 上的函数
上的函数 ,使当
,使当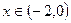 时,
时, ,当
,当 时,
时, (b、c、d为常数),当
(b、c、d为常数),当 时,
时, 只有一个实根,当
只有一个实根,当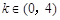 时,
时, 有2个极值点;②函数
有2个极值点;②函数 有一个相同的实根;④
有一个相同的实根;④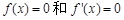 有一个相同的实根。
有一个相同的实根。 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围; 的导函数为
的导函数为 ,且
,且 ,则
,则 等于 ( )
等于 ( )



 ,若
,若 ,则
,则 ( )
( )



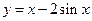 在
在 上的单调递增区间为
上的单调递增区间为