题目内容
甲乙丙三位棋手按如下规则进行比赛:第一局由甲乙参加而丙轮空,由第一局的胜者与丙进行第二局比赛,败者轮空,使用这种方式一直进行到其中一人连胜两局为止,此人成为整场比赛的优胜者.甲乙丙胜各局的概率都为0.5,求甲乙丙分别成为整场比赛优胜者的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:利用无穷递缩等比数列的各项和的求法求得甲可以在第2局获胜,即开始两局(第1局和第2局)连续获胜,还可以在第5局,第8局,…第3n-1局获胜的概率,再求得甲在第4局获胜,即前两局没人获胜,第3局和第4局甲连胜,以后还可以在第7局,第10局,…第3n+1局获胜的概率,再把这2个概率相加,即得所求.
解答:
解:按此规则,甲如果获胜,可以分成两类:
(1)甲可以在第2局获胜,即开始两局(第1局和第2局)连续获胜,还可以在第5局,第8局,…第3n-1局获胜(第n轮,每三场比赛为一轮),
其概率为:P=
=
(无穷递缩等比数列所有项之和,首项
,公比
).
(2)甲还可以在第4局获胜,即前两局没人获胜,第3局和第4局甲连胜,以后还可以在第7局,第10局,…第3n+1局获胜,其概率为:
P=
=
(无穷递缩等比数列所有项之和,首项
,公比
);所以甲获胜的概率为:
+
,
而乙与甲获胜概率相等,也为
,因此丙获胜的概率为:
.
(1)甲可以在第2局获胜,即开始两局(第1局和第2局)连续获胜,还可以在第5局,第8局,…第3n-1局获胜(第n轮,每三场比赛为一轮),
其概率为:P=
| ||
1-
|
| 2 |
| 7 |
| 1 |
| 4 |
| 1 |
| 8 |
(2)甲还可以在第4局获胜,即前两局没人获胜,第3局和第4局甲连胜,以后还可以在第7局,第10局,…第3n+1局获胜,其概率为:
P=
| ||
1-
|
| 1 |
| 14 |
| 1 |
| 16 |
| 1 |
| 8 |
| 2 |
| 7 |
| 1 |
| 14 |
| 5 |
| 14 |
而乙与甲获胜概率相等,也为
| 5 |
| 14 |
| 4 |
| 14 |
点评:本题主要考查无穷递缩等比数列的各项和的求法,互斥事件的概率加法公式、相互独立事件的概率乘法公式的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
若平面向量
=(1,x)和
=(2x+3,-x)互相平行,其中x∈R,则|
-
|=( )
| a |
| b |
| a |
| b |
| A、-2或0 | ||
| B、2.5 | ||
C、2或2
| ||
| D、2或10 |
设点O是△ABC的外心,AB=13,AC=12,则
•
为( )
| BC |
| AO |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
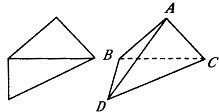 如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.
如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.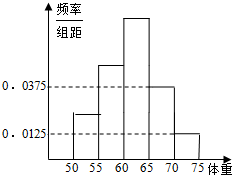 为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )
为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )