题目内容
8．若tanα=3，tanβ=$\frac{4}{3}$，则$\frac{1}{tan（α-β）}$等于（ ）| A． | -3 | B． | -$\frac{1}{3}$ | C． | 3 | D． | $\frac{1}{3}$ |
分析 根据两角差的正切公式进行计算即可．
解答 解：∵tanα=3，tanβ=$\frac{4}{3}$，
∴$\frac{1}{tan（α-β）}$=$\frac{1+tanα•tanβ}{tanα-tanβ}$
=$\frac{1+3×\frac{4}{3}}{3-\frac{4}{3}}$
=3．
故选：C．
点评 本题考查了两角差的正切公式的应用问题，是基础题目．
练习册系列答案
相关题目
18．双曲线C的渐近线方程为y=±$\sqrt{2}$x，则C的离心率为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{6}$ | C． | $\frac{\sqrt{6}}{2}$或$\sqrt{6}$ | D． | $\sqrt{3}$或$\frac{\sqrt{6}}{2}$ |
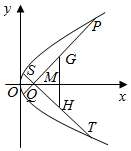已知抛物线C：y2=2px（p＞0）的焦点是F，点D（1，y0）是抛物线C上的点，且|DF|=3．
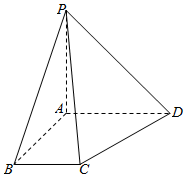如图，在四棱锥P-ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC=∠BAD=90°，AB=AD=AP=2，BC=1．求：