题目内容
11.已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,过O作直线AB的垂线,垂足为P,若|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=$\sqrt{3}$,∠AOB=$\frac{π}{6}$,$\overrightarrow{OP}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则x-y=-2.
分析 由$\overrightarrow{OP}$•$\overrightarrow{AB}$=0可得3x+y=0,再由余弦定理及三角形面积公式可得|$\overrightarrow{OP}$|=$\frac{3}{2}$,从而可得(x$\overrightarrow{a}$+y$\overrightarrow{b}$)•(x$\overrightarrow{a}$+y$\overrightarrow{b}$)=$\frac{9}{4}$,从而结合图象解得.
解答 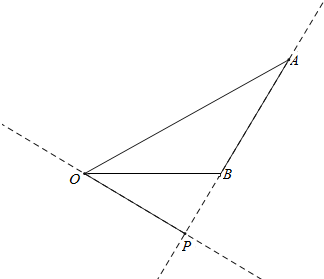 解:$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
解:$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∵$\overrightarrow{OP}$•$\overrightarrow{AB}$=0,
∴(x$\overrightarrow{a}$+y$\overrightarrow{b}$)•($\overrightarrow{b}$-$\overrightarrow{a}$)=0,
∴x$\overrightarrow{a}$•$\overrightarrow{b}$-x$\overrightarrow{a}$•$\overrightarrow{a}$+y$\overrightarrow{b}$•$\overrightarrow{b}$-y$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即x•3•$\sqrt{3}$•cos$\frac{π}{6}$-9x+3y-y•3•$\sqrt{3}$•cos$\frac{π}{6}$=0,
故$\frac{9}{2}$x-9x+3y-$\frac{9}{2}$y=0,
故3x+y=0,
∵AB2=OA2+OB2-2OA•OB•cos$\frac{π}{6}$=3,
∴AB=$\sqrt{3}$,
∴$\frac{1}{2}$|$\overrightarrow{a}$||$\overrightarrow{b}$|•sin$\frac{π}{6}$=$\frac{1}{2}$|$\overrightarrow{OP}$|•$\sqrt{3}$,
即|$\overrightarrow{OP}$|=$\frac{3}{2}$,
即(x$\overrightarrow{a}$+y$\overrightarrow{b}$)•(x$\overrightarrow{a}$+y$\overrightarrow{b}$)=$\frac{9}{4}$,
即9x2+3y2+9xy=$\frac{9}{4}$,
结合图象可知,x<0,
解得,x=-$\frac{1}{2}$,y=$\frac{3}{2}$,
故x-y=-2,
故答案为:-2.
点评 本题考查了平面向量与解三角形的综合应用,同时考查了数形结合的思想应用.

| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
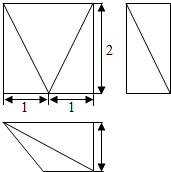
| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
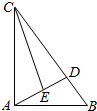 如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3}{2}$ |
| A. | y2=8$\sqrt{2}$x | B. | y2=±4$\sqrt{2}$x | C. | y2=±4x | D. | y2=±8$\sqrt{2}$x |
 在一次全国高中五省大联考中,有90万的学生参加,考后对所有学生成绩统计发现,英语成绩服从正态分布N(μ,σ2),如表用茎叶图列举了20名学生英语的成绩,巧合的是这20个数据的平均数和方差恰比所有90万个数据的平均数和方差都多0.9,且这20个数据的方差为49.9.
在一次全国高中五省大联考中,有90万的学生参加,考后对所有学生成绩统计发现,英语成绩服从正态分布N(μ,σ2),如表用茎叶图列举了20名学生英语的成绩,巧合的是这20个数据的平均数和方差恰比所有90万个数据的平均数和方差都多0.9,且这20个数据的方差为49.9.