题目内容
下列函数中,满足f(x2)=[f(x)]2的是
- A.f(x)=lnx
- B.f(x)=|x+1|
- C.f(x)=x3
- D.f(x)=ex
C
分析:利用指数的运算性质及对数的运算性质,分别求出f(x2)与[f(x)]2,比照后,可得答案.
解答:若f(x)=lnx,则f(x2)=lnx2=2lnx,[f(x)]2=(lnx)2,不满足f(x2)=[f(x)]2,
若f(x)=|x+1|,则f(x2)=|x2+1|,[f(x)]2=|x+1|2=x2+2x+1,不满足f(x2)=[f(x)]2,
若f(x)=x3,则f(x2)=(x2)3=x6,[f(x)]2=(x3)2=x6,满足f(x2)=[f(x)]2,
若f(x)=ex,则f(x2)=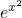 ,[f(x)]2=(ex)2=e2x,不满足f(x2)=[f(x)]2,
,[f(x)]2=(ex)2=e2x,不满足f(x2)=[f(x)]2,
故选C
点评:本题考查的知识点函数解析式的求解,熟练掌握指数的运算性质及对数的运算性质,分别求出f(x2)与[f(x)]2,是解答的关键.
分析:利用指数的运算性质及对数的运算性质,分别求出f(x2)与[f(x)]2,比照后,可得答案.
解答:若f(x)=lnx,则f(x2)=lnx2=2lnx,[f(x)]2=(lnx)2,不满足f(x2)=[f(x)]2,
若f(x)=|x+1|,则f(x2)=|x2+1|,[f(x)]2=|x+1|2=x2+2x+1,不满足f(x2)=[f(x)]2,
若f(x)=x3,则f(x2)=(x2)3=x6,[f(x)]2=(x3)2=x6,满足f(x2)=[f(x)]2,
若f(x)=ex,则f(x2)=
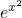 ,[f(x)]2=(ex)2=e2x,不满足f(x2)=[f(x)]2,
,[f(x)]2=(ex)2=e2x,不满足f(x2)=[f(x)]2,故选C
点评:本题考查的知识点函数解析式的求解,熟练掌握指数的运算性质及对数的运算性质,分别求出f(x2)与[f(x)]2,是解答的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目