题目内容
13.已知如图所示向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$,求作向量$\overrightarrow{l}$,使得$\overrightarrow{l}$=3$\overrightarrow{a}$-$\overrightarrow{b}$+2$\overrightarrow{c}$,并将向量$\overrightarrow{c}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{l}$线性表示.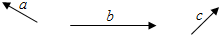
分析 根据向量加减法的几何意义作图,根据$\overrightarrow{l}$=3$\overrightarrow{a}$-$\overrightarrow{b}$+2$\overrightarrow{c}$得出$\overrightarrow{c}$.
解答 解:做$\overrightarrow{AB}=3\overrightarrow{a}$,$\overrightarrow{BC}=2\overrightarrow{c}$,$\overrightarrow{AD}=\overrightarrow{b}$,则$\overrightarrow{DC}$=$\overrightarrow{AB}+\overrightarrow{BC}-\overrightarrow{AD}$=3$\overrightarrow{a}$-$\overrightarrow{b}$+2$\overrightarrow{c}$,
∴$\overrightarrow{DC}$即为所求向量$\overrightarrow{l}$.
∵$\overrightarrow{l}$=3$\overrightarrow{a}$-$\overrightarrow{b}$+2$\overrightarrow{c}$,∴$\overrightarrow{c}$=$-\frac{3}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{l}$.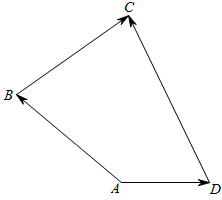
点评 本题考查了向量线性运算的几何意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知函数f(x)=ax2+bx+1具有以下性质:
①对任意实数x1≠x2,且f(x1)=f(x2)时,满足x1+x2=2.
②对任意x1,x2∈(1,+∞)上,总有f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$.
则方程ax2+bx+1=0根的情况是( )
①对任意实数x1≠x2,且f(x1)=f(x2)时,满足x1+x2=2.
②对任意x1,x2∈(1,+∞)上,总有f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$.
则方程ax2+bx+1=0根的情况是( )
| A. | 无实数根 | B. | 有两个不等正根 | C. | 有两个异号实根 | D. | 有两个相等正根 |
8.若数列{an}是递增数列,并且an=n2-2tn,则t的取值范围是( )
| A. | (-∞,0) | B. | (-∞,1) | C. | (0,2) | D. | (-∞,$\frac{3}{2}$) |
14.已知函数f(x)在(0,$\frac{π}{2}$)上处处可导,若[f(x)-f′(x)]tanx-f(x)<0,则( )
| A. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$一定小于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| B. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$一定大于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| C. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$可能大于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| D. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$可能等于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ |