题目内容
设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,则公比q=
-
| 3 |
| ||
-
.| 3 |
| ||
分析:设出等比数列的首项和公比,由S3,S9,S6成等差数列列式求解q的值.
解答:解:设等比数列{an}的首项为a1,公比为q,
由S3,S9,S6成等差数列,知q≠1,且2S9=S3+S6,
即2
=
+
整理得:2q6+q3=0,解得q=-
.
故答案为-
.
由S3,S9,S6成等差数列,知q≠1,且2S9=S3+S6,
即2
| a1(1-q9) |
| 1-q |
| a1(1-q3) |
| 1-q |
| a1(1-q6) |
| 1-q |
整理得:2q6+q3=0,解得q=-
| 3 |
| ||
故答案为-
| 3 |
| ||
点评:本题考查了等比数列的前n项和,考查了等差数列的通项公式,考查了学生的计算能力,是基础的计算题.

练习册系列答案
相关题目
设Sn是等比数列{an}的前n项和,
=
,则
等于( )
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 的前n项和,若
的前n项和,若 ,则
,则 ( )
( )  B、
B、 C、
C、 D、
D、
 ,则
,则 等于( )
等于( )



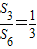 ,则
,则 等于( )
等于( )


