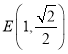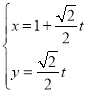题目内容
【题目】在平面直角坐标系
中，已知
，动点
满足
.
（1）求动点的轨迹
的方程；
（2）若点M为（1）中轨迹上一动点，
，直线MA与的另一个交点为N；记
，若t值与点M位置无关，则称此时的点A为“稳定点”.是否存在 “稳定点”？若存在，求出该点；若不存在，请说明理由.
【答案】（1）
；（2）答案不唯一，答案见解析.
【解析】
（1）设
，运用向量的坐标运算并化简，求得动点
的轨迹
的方程；
（2）设
，设直线
的方程为
，与轨迹联立，并表示出根与系数的关系，将
化简得
，分
和
去绝对值，看是否存在t值与点M位置无关.
解：（1）设，则
由
可知：
，化简得
即动点的轨迹的方程为：
（2）设，设直线的方程为，联立
得
.
.
则
则
①当时，
同号，
，
不论
取何值，
均与
有关，即时，
不是“稳定点”.
②当时，
异号.
又
当且仅当
,即
时，与无关，此时的点
为“稳定点”.
练习册系列答案
相关题目
