题目内容
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,过
的焦点,过![]() 的动直线交抛物线
的动直线交抛物线![]() 于
于![]() ,
,![]() 两点.当直线与
两点.当直线与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 的斜率为1且与抛物线的准线
的斜率为1且与抛物线的准线![]() 相交于点
相交于点![]() ,抛物线
,抛物线![]() 上存在点
上存在点![]() 使得直线
使得直线![]() ,
,![]() ,
,![]() 的斜率成等差数列,求点
的斜率成等差数列,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意可得![]() ,即可求出抛物线的方程,
,即可求出抛物线的方程,
(2)设直线![]() 的方程为
的方程为![]() ,联立
,联立 消去
消去![]() ,得
,得![]() ,根据韦达定理结合直线
,根据韦达定理结合直线![]() ,
,![]() ,
,![]() 的斜率成等差数列,即可求出点
的斜率成等差数列,即可求出点![]() 的坐标
的坐标
解:(1)因为![]() ,在抛物线方程
,在抛物线方程![]() 中,令
中,令![]() ,可得
,可得![]() .
.
于是当直线与![]() 轴垂直时,
轴垂直时,![]() ,解得
,解得![]() .
.
所以抛物线的方程为![]() .
.
(2)因为抛物线![]() 的准线方程为
的准线方程为![]() ,所以
,所以![]() .
.
设直线![]() 的方程为
的方程为![]() ,
,
联立 消去
消去![]() ,得
,得![]() .
.
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
若点![]() ,
,![]() 满足条件,则
满足条件,则![]() ,
,
即![]() ,
,
因为点![]() ,
,![]() ,
,![]() 均在抛物线上,所以
均在抛物线上,所以![]() .
.
代入化简可得![]() ,
,
将![]() ,
,![]() 代入,解得
代入,解得![]() .
.
将![]() 代入抛物线方程,可得
代入抛物线方程,可得![]() .
.
于是点![]() 为满足题意的点.
为满足题意的点.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】为了提高生产效益,某企业引进了一批新的生产设备,为了解设备生产产品的质量情况,分别从新、旧设备所生产的产品中,各随机抽取100件产品进行质量检测,所有产品质量指标值均在![]() 以内,规定质量指标值大于30的产品为优质品,质量指标值在
以内,规定质量指标值大于30的产品为优质品,质量指标值在![]() 的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
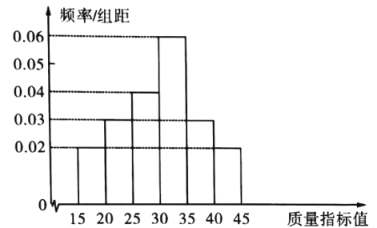
质量指标值 | 频数 |
| 2 |
| 8 |
| 20 |
| 30 |
| 25 |
| 15 |
合计 | 100 |
(1)请分别估计新、旧设备所生产的产品的优质品率.
(2)优质品率是衡量一台设备性能高低的重要指标,优质品率越高说明设备的性能越高,根据已知图表数据填写下面列联表(单位:件),并判断是否有![]() 的把握认为“产品质量高于新设备有关”.
的把握认为“产品质量高于新设备有关”.
非优质品 | 优质品 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
附:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
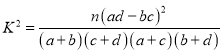 ,其中
,其中![]() .
.
(3)已知每件产品的纯利润y(单位:元)与产品质量指标值t的关系式为![]() 若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.