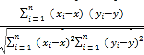题目内容
【题目】已知椭圆C1：
(a>b>0)的右焦点F与抛物线C2的焦点重合，C1的中心与C2的顶点重合．过F且与x轴重直的直线交C1于A，B两点，交C2于C，D两点，且|CD|=
|AB|．
（1）求C1的离心率；
（2）若C1的四个顶点到C2的准线距离之和为12，求C1与C2的标准方程．
【答案】（1）
；（2）
：
，
： 
.
【解析】
（1）根据题意求出的方程，结合椭圆和抛物线的对称性不妨设
在第一象限，运用代入法求出
点的纵坐标，根据
，结合椭圆离心率的公式进行求解即可；
（2）由（1）可以得到椭圆的标准方程，确定椭圆的四个顶点坐标，再确定抛物线的准线方程，最后结合已知进行求解即可；
解：（1）因为椭圆的右焦点坐标为：
,所以抛物线的方程为
，其中
.
不妨设在第一象限，因为椭圆的方程为：
，
所以当
时，有
，因此
的纵坐标分别为
，
；
又因为抛物线的方程为，所以当时，有
，
所以
的纵坐标分别为
，
，故
，
.
由得
，即
，解得
（舍去），
.
所以的离心率为.
（2）由（1）知
，
，故
，所以的四个顶点坐标分别为
，
，
，
，的准线为
.
由已知得
，即
.
所以的标准方程为，的标准方程为.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
