题目内容

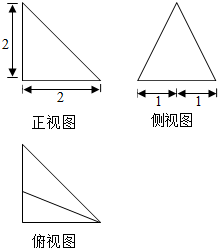
15．一个几何体的三视图如图所示，则该几何体的表面积是（　　）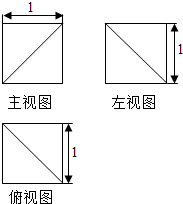
A．$\frac{{9+\sqrt{3}}}{2}$B．5C．$\frac{{18+\sqrt{3}}}{4}$D．$4+\sqrt{2}$

分析 几何体为边长为1的正方体切去一个三棱锥得到的，共含有7个面．

解答 解：由三视图可知该几何体为边长为1的正方体切去一个三棱锥得到的，三棱锥的底面边长为正方体相邻三个面的对角线长，
剩余几何体有3个面为原正方体的面，有3个面为原正方体面的一半，有1个面为等边三角形，边长为原正方体的面对角线长．
∴几何体的表面积为1×3+$\frac{1}{2}×3$+$\frac{\sqrt{3}}{4}×$（$\sqrt{2}$）2=$\frac{9+\sqrt{3}}{2}$．
故选A．

点评 本题考查了空间几何体的三视图和体积计算，属于基础题．

练习册系列答案
相关题目
5．某几何体的三视图如图所示，则该几何体的表面积为（　　）
A．1B．21+$\sqrt{3}$C．3$\sqrt{3}$+12D．$\frac{3\sqrt{3}}{2}$+12
6．一个三棱锥的三视图如图所示，则其体积是$\frac{4}{3}$；此三棱锥的最长棱的长度为3．
3．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°，且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，那么$\overrightarrow{b}$•（2$\overrightarrow{a}$-$\overrightarrow{b}$）的值为（　　）
A．-8B．-6C．0D．4
10．已知抛物线C：y2=2px（p＞0），过点A（12，0）作直线MN垂直x轴交抛物线于M、N两点，ME⊥ON于E，AE∥OM，O为坐标原点．
（Ⅰ）求p的值；
（Ⅱ）是否存在直线l与抛物线C交于G、H两点，且F（2，-2）是GH的中点．若存在求出直线l方程；若不存在，请说明理由．
20．椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$的左、右焦点分别为F1，F2，弦AB过F1，若△ABF2的内切圆周长为4，A、B两点的坐标分别为（x1，y1）和（x2，y2），则|y2-y1|的值为（　　）
A．$\frac{\sqrt{5}}{3}$B．$\frac{10}{3}$C．$\frac{20}{3}$D．$\frac{5}{3}$
7．已知某几何体的三视图如图，根据图中标出的尺寸（单位cm），可得这个几何体的体积是$\frac{8}{3}$cm3．
4．已知抛物线C的焦点M，其准线与x轴的交点为K，过点K（-1，0）的直线l与C交于A，B两点，点A关于x轴的对称点为D．
（Ⅰ）证明：点F在直线BD上；
（Ⅱ）设$\overrightarrow{FA}$•$\overrightarrow{FB}$=$\frac{8}{9}$，求△BDK内切圆M的方程．
5．如图所示程序框图，输出的结果是（　　）
A．2B．3C．4D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网