题目内容
17.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,若$\overrightarrow{a}$+$\overrightarrow{b}$垂直于y轴,且满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,$\overrightarrow{b}$=(2,-1),则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为-$\frac{3\sqrt{2}}{2}$或-$\frac{7\sqrt{10}}{10}$.分析 设$\overrightarrow{a}$=(m,n),由题意可得n=1,再由向量的模的公式,可得m=-1或-3,再由$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$,计算即可得到所求.
解答 解:设$\overrightarrow{a}$=(m,n),由$\overrightarrow{b}$=(2,-1),
$\overrightarrow{a}$+$\overrightarrow{b}$垂直于y轴,可得n=1,
又|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,可得|m+2|=1,
解得m=-1或-3,
即有$\overrightarrow{a}$=(-1,1)或(-3,1),
则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{-2-1}{\sqrt{2}}$=-$\frac{3\sqrt{2}}{2}$;
或$\frac{-6-1}{\sqrt{10}}$=-$\frac{7\sqrt{10}}{10}$.
故答案为:-$\frac{3\sqrt{2}}{2}$或-$\frac{7\sqrt{10}}{10}$.
点评 本题考查向量的投影的求法,注意运用向量的数量积和模的公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.已知tan(-$\frac{14π}{15}$)=a,那么sin1992°等于( )
| A. | $\frac{|a|}{\sqrt{1+{a}^{2}}}$ | B. | $\frac{a}{\sqrt{1+{a}^{2}}}$ | C. | -$\frac{a}{\sqrt{1+{a}^{2}}}$ | D. | -$\frac{1}{\sqrt{1+{a}^{2}}}$ |
9.已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,y≤$\sqrt{x}$},若向区域Ω上随机投一点P,则点P落入区域A的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{8}{27}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
6.A、B、C、D.E、F共6人站成一排照相,要求A不站在两侧,而且B、C两人站在一起,那么不同的站法种数为( )
| A. | 72 | B. | 96 | C. | 144 | D. | 288 |
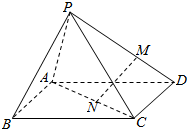 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB. 一个容量为200的样本频率分布直方图如图所示,则样本数据落在范围[5,9)的频率和频数分别为0.2和180.
一个容量为200的样本频率分布直方图如图所示,则样本数据落在范围[5,9)的频率和频数分别为0.2和180.