题目内容
已知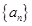 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项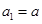 ,
,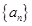 的部分项
的部分项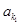 、
、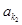 、 、
、 、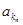 恰为等比数列,且
恰为等比数列,且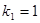 ,
,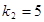 ,
,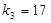 .
.
(1)求数列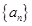 的通项公式
的通项公式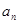 (用
(用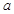 表示);
表示);
(2)设数列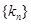 的前
的前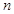 项和为
项和为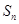 , 求证:
, 求证: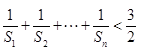 (
(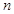 是正整数
是正整数
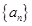 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项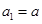 ,
,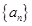 的部分项
的部分项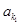 、
、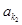 、 、
、 、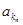 恰为等比数列,且
恰为等比数列,且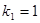 ,
,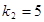 ,
,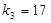 .
.(1)求数列
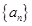 的通项公式
的通项公式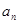 (用
(用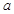 表示);
表示);(2)设数列
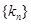 的前
的前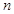 项和为
项和为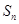 , 求证:
, 求证: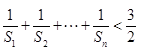 (
(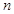 是正整数
是正整数(1)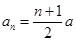 (2)见解析
(2)见解析
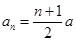 (2)见解析
(2)见解析试题分析:
(1)由题得a1,a5,a17是成等比数列的,所以
 ,则可以利用公差d和首项a来表示
,则可以利用公差d和首项a来表示 ,进而得到d的值,得到an的通项公式.
,进而得到d的值,得到an的通项公式.(2)利用第一问可以求的等比数列
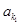 、
、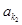 、 、
、 、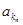 中的前三项,得到该等比数列的通项公式,进而得到
中的前三项,得到该等比数列的通项公式,进而得到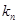 的通项公式,再利用分组求和法可得到Sn的表达式,可以发现
的通项公式,再利用分组求和法可得到Sn的表达式,可以发现 为不可求和数列,所以需要把
为不可求和数列,所以需要把 放缩成为可求和数列,考虑利用
放缩成为可求和数列,考虑利用 的二项式定理放缩证明
的二项式定理放缩证明 ,即
,即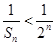 ,故求和即可证明原不等式.
,故求和即可证明原不等式.试题解析:
(1)设数列
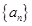 的公差为
的公差为 ,
,由已知得
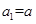 ,
, ,
,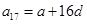 成等比数列,
成等比数列,∴

 ,且
,且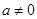 2分
2分得
 或
或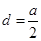
∵ 已知
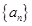 为公差不为零
为公差不为零∴
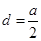 , 3分
, 3分∴
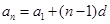
 . 4分
. 4分(2)由(1)知
 ∴
∴ 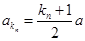 5分
5分而等比数列
 的公比
的公比 .
.∴
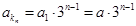 6分
6分因此
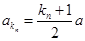
 ,
,∵
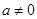
∴
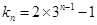 7分
7分∴


 9分
9分∵当
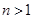 时,
时,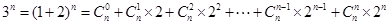


∴
 (或用数学归纳法证明此不等式)
(或用数学归纳法证明此不等式)∴

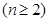 11分
11分∴当
 时,
时, ,不等式成立;
,不等式成立;当
 时,
时,


综上得不等式

 成立. 14分
成立. 14分法二∵当
 时,
时,
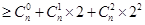

∴
 (或用数学归纳法证明此不等式)
(或用数学归纳法证明此不等式)∴

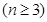 11分
11分∴当
 时,
时, ,不等式成立;
,不等式成立;当
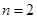 时,
时, ,不等式成立;
,不等式成立;当
 时,
时,
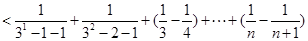
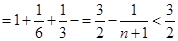
综上得不等式

 成立. 14分
成立. 14分(法三) 利用二项式定理或数学归纳法可得:

所以,
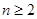 时,
时,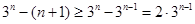 ,
,
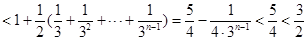
 时,
时, 综上得不等式
综上得不等式
 成立.
成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
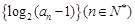 为等差数列,且
为等差数列,且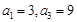 .
.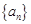 的通项公式;
的通项公式;
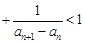 .
.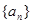 的公差不为零,其前n项和为
的公差不为零,其前n项和为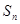 ,若
,若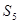 =70,且
=70,且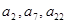 成等比数列,
成等比数列,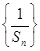 的前n项和为
的前n项和为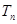 ,求证:
,求证: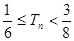 .
.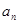 }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.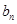 =
=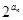 ,求数列{
,求数列{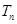 .
.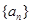 ,其前
,其前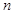 项和
项和 满足
满足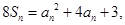 且
且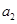 是
是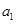 和
和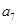 的等比中项..
的等比中项..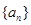 的通项公式;
的通项公式;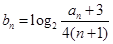 ,求数列
,求数列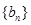 的前99项和.
的前99项和.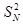 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.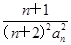 ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<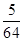 .
.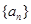 的前n项和为
的前n项和为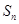 ,且
,且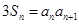 ,则
,则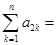 ( )
( )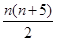
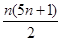
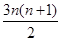

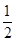 .
.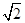 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.