题目内容
已知数列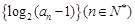 为等差数列,且
为等差数列,且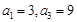 .
.
(1)求数列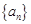 的通项公式;
的通项公式;
(2)证明
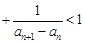 .
.
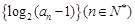 为等差数列,且
为等差数列,且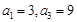 .
.(1)求数列
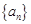 的通项公式;
的通项公式;(2)证明

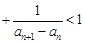 .
.(1) ;(2)
;(2)
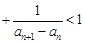 .
.
 ;(2)
;(2)
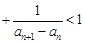 .
.试题分析:(1)先利用等差数列的定义有
 ,
, 时计算得
时计算得 ,再将
,再将 代入上式得
代入上式得 ;
;(2)先将
 代入分式化简,得通项
代入分式化简,得通项 ,
,这说明该求和数列可以看作首项为
 ,公比等于
,公比等于 的等比数列,项数注意应为
的等比数列,项数注意应为 项,再利用等比数列求和公式计算得
项,再利用等比数列求和公式计算得 ,而
,而 ,故
,故 .
.试题解析:(1)设等差数列的公差为
 ,由
,由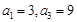 得
得 即
即 ; 3分
; 3分所以
 即
即 ; 6分
; 6分(2)证明:
 , 8分
, 8分

 . 12分
. 12分
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的前n项和为
的前n项和为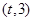 ,
,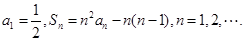
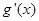 ;
;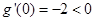 ,求证:
,求证: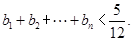
 是公差不等于0的等差数列,
是公差不等于0的等差数列,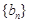 是等比数列
是等比数列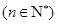 ,且
,且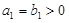 .
.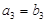 ,比较
,比较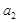 与
与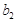 的大小关系;
的大小关系;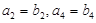 .(ⅰ)判断
.(ⅰ)判断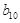 是否为数列
是否为数列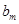 是数列
是数列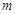 的集合(不必说明理由).
的集合(不必说明理由).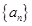 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项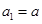 ,
,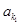 、
、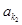 、 、
、 、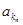 恰为等比数列,且
恰为等比数列,且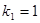 ,
,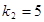 ,
,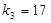 .
.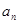 (用
(用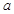 表示);
表示);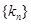 的前
的前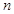 项和为
项和为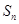 , 求证:
, 求证: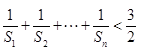 (
( 的前
的前 项和为
项和为 ,若
,若 ,则
,则



 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( ) 中,若公差
中,若公差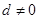 ,且
,且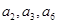 成等比数列,则公比
成等比数列,则公比 .
. 的前项和为
的前项和为 ,若
,若 ,
, ,则
,则 等于 .
等于 . 的前
的前 项和为
项和为 ,则
,则