题目内容
锐角△ABC中,角A、B、C对边a、b、c,c=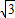 ,b=1,∠B=30°,则△ABC的面积等于 .
,b=1,∠B=30°,则△ABC的面积等于 .
【答案】分析:利用余弦定理求出a边长,代入三角形面积公式S= ac•sinB可得答案.
ac•sinB可得答案.
解答:解:∵c=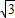 ,b=1,∠B=30°,
,b=1,∠B=30°,
由余弦定理可得
b2=a2+c2-2•a•c•cosB
即1=a2+3-3a
即a2-3a+2=0
解得a=1或a=2
∴△ABC的面积S= ac•sinB=
ac•sinB=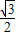 或
或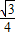
故答案为: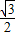 或
或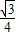
点评:本题考查的知识点是三角形的面积公式,余弦定理,其中根据余弦定理求出a长是解答的关键.
 ac•sinB可得答案.
ac•sinB可得答案.解答:解:∵c=
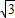 ,b=1,∠B=30°,
,b=1,∠B=30°,由余弦定理可得
b2=a2+c2-2•a•c•cosB
即1=a2+3-3a
即a2-3a+2=0
解得a=1或a=2
∴△ABC的面积S=
 ac•sinB=
ac•sinB=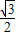 或
或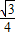
故答案为:
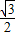 或
或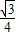
点评:本题考查的知识点是三角形的面积公式,余弦定理,其中根据余弦定理求出a长是解答的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
锐角△ABC中,角A、B、C所对的边分别为a、b、c,C=2A,
的取值范围是( )
| c |
| a |
| A、(1,2) | ||||
B、(1,
| ||||
C、(
| ||||
D、(
|