题目内容
已知数列{an}的前n项和为Sn,a1=1,an+1=
Sn.求证:
(1)数列{
}成等比;
(2)Sn+1=4an.
| n+2 |
| n |
(1)数列{
| Sn |
| n |
(2)Sn+1=4an.
考点:数列递推式,等比关系的确定
专题:等差数列与等比数列
分析:(1)由an+1=
Sn,知Sn-Sn-1=
-
,从而
=
,进而
=
,(n≥2),由此能证明{
}是首项为1,公比为2的等比数列.
(2)由(1)可知Sn=n•2n-1,an=(n+1)•2n-2.由此能证明Sn+1=(n+1)•2n=4an.
| n+2 |
| n |
| nan+1 |
| n+2 |
| (n-1)an |
| n+1 |
| 2an |
| n+1 |
| an+1 |
| n+2 |
| 2Sn-1 |
| n-1 |
| Sn |
| n |
| Sn |
| n |
(2)由(1)可知Sn=n•2n-1,an=(n+1)•2n-2.由此能证明Sn+1=(n+1)•2n=4an.
解答:
证明:(1)∵数列{an}的前n项和为Sn,a1=1,an+1=
Sn,
∴Sn=
,Sn-1=
,n≥2
∴an=Sn-Sn-1=
-
,
即2n×
=
,
∵n≠0,∴
=
,
∴
=
,(n≥2)
即
:
=2,
n=1时,
=
=1,
∴{
}是首项为1,公比为2的等比数列.
(2)∵{
}是首项为1,公比为2的等比数列,
∴
=2n-1,∴Sn=n•2n-1,
∴an+1=
Sn=n•2n-1×
=(n+2)•2n-1,
∴an=(n+1)•2n-2.
∴Sn+1=(n+1)•2n=4an.
| n+2 |
| n |
∴Sn=
| nan+1 |
| n+2 |
| (n-1)an |
| n+1 |
∴an=Sn-Sn-1=
| nan+1 |
| n+2 |
| (n-1)an |
| n+1 |
即2n×
| an |
| n+1 |
| nan+1 |
| n+2 |
∵n≠0,∴
| 2an |
| n+1 |
| an+1 |
| n+2 |
∴
| 2Sn-1 |
| n-1 |
| Sn |
| n |
即
| Sn |
| n |
| Sn-1 |
| n-1 |
n=1时,
| S1 |
| 1 |
| a1 |
| 1 |
∴{
| Sn |
| n |
(2)∵{
| Sn |
| n |
∴
| Sn |
| n |
∴an+1=
| n+2 |
| n |
| n+2 |
| n |
∴an=(n+1)•2n-2.
∴Sn+1=(n+1)•2n=4an.
点评:本题考查等比数列的证明,考查Sn+1=4an的证明,解题时要认真审题,注意构造法的合理运用,是中档题.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
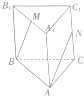 已知正三棱柱ABC-A1B1C1的底面边长是2,侧棱长为4,M、N分别是A1B1,CC1中点,则AN与BM所成角的余弦值为( )
已知正三棱柱ABC-A1B1C1的底面边长是2,侧棱长为4,M、N分别是A1B1,CC1中点,则AN与BM所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
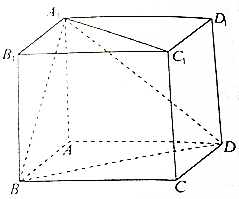 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: