题目内容
直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的方程为
 ,直线
,直线 方程为
方程为 (t为参数),直线
(t为参数),直线 与C的公共点为T.
与C的公共点为T.
(1)求点T的极坐标;
(2)过点T作直线 ,
, 被曲线C截得的线段长为2,求直线
被曲线C截得的线段长为2,求直线 的极坐标方程.
的极坐标方程.
(1) ;(2)
;(2) 或
或 .
.
解析试题分析:解题思路:(1将曲线方程化成直角坐标方程,再将直线方程代入曲线方程,得到关于 的方程即可;(2)先利用直角坐标系中的直线与圆的位置关系求直线方程,再化成极坐标方程.规律总结:涉及直线与曲线的极坐标方程、参数方程的问题,要注意极坐标方程、参数方程与直角坐标方程的相互转化.
的方程即可;(2)先利用直角坐标系中的直线与圆的位置关系求直线方程,再化成极坐标方程.规律总结:涉及直线与曲线的极坐标方程、参数方程的问题,要注意极坐标方程、参数方程与直角坐标方程的相互转化.
试题解析:(1)曲线 的直角坐标方程
的直角坐标方程 .
.
将 代入上式并整理得
代入上式并整理得 .
.
解得 .
. 点T的坐标为(1,
点T的坐标为(1, ).
).
其极坐标为(2, ) .
) .
(2)设直线 的方程
的方程
由(1)得曲线C是以(2,0)为圆心的圆,且圆心到直线 .
.
则
直线 的方程为
的方程为 ,或
,或 .
.
其极坐标方程为 或
或 .
.
考点:1.极坐标方程;2.参数方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 化为直角坐标方程是________________
化为直角坐标方程是________________  轴正半轴,直线
轴正半轴,直线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为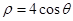 .
. 、
、 两点,求
两点,求 .
. 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线 的方程为
的方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 ,若曲线
,若曲线 、
、 两点.
两点. 的值;
的值; 到
到 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .求:
.求: 的直角坐标方程;
的直角坐标方程; 是直线
是直线 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围. 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C. 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与 垂直的直线的极坐标方程.
垂直的直线的极坐标方程. 的极坐标方程为
的极坐标方程为 ,直线
,直线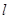 的参数方程为
的参数方程为
 为参数),点
为参数),点 的极坐标为
的极坐标为 ,设直线
,设直线 、
、 .
. 的值.
的值.  轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为
轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为 (
( 为参数),点Q的极坐标为
为参数),点Q的极坐标为 。
。 过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线
过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线 (
( 为参数)与曲线
为参数)与曲线 的直角坐标方程分别为 , ,两条曲线的交点个数为 个.
的直角坐标方程分别为 , ,两条曲线的交点个数为 个.