题目内容
7.若不等式(-1)na<2+$\frac{1}{n}$(-1)n+1对?n∈N*恒成立,则实数a的取值范围是[-2,$\frac{3}{2}$].分析 若n为正奇数,-a<2+$\frac{1}{n}$恒成立?-a<(2+$\frac{1}{n}$)min,可解得:a≥-2;若n为正偶数,a<2-$\frac{1}{n}$恒成立?-a<(2-$\frac{1}{n}$)min,利用函数的单调性可得a≤$\frac{3}{2}$.从而可得答案.
解答 解:若n为正奇数,则-a<2+$\frac{1}{n}$恒成立?-a<(2+$\frac{1}{n}$)min,由于y=2+$\frac{1}{n}$为减函数,当n→+∞时,y→0,故-a≤2,解得:a≥-2;
若n为正偶数,则a<2-$\frac{1}{n}$恒成立?-a<(2-$\frac{1}{n}$)min,由于y=2-$\frac{1}{n}$为增函数,当n=2时,y=2-$\frac{1}{n}$取得最小值(2-$\frac{1}{2}$)=$\frac{3}{2}$,故a≤$\frac{3}{2}$.
因为不等式(-1)na<2+$\frac{1}{n}$(-1)n+1对?n∈N*恒成立,
所以,-2≤a≤$\frac{3}{2}$.
故答案为:[-2,$\frac{3}{2}$].
点评 本题考查函数恒成立问题,考查分类讨论思想与等价转化思想的综合运用,考查逻辑思维能力与运算求解能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.马云同学向某银行贷款M万元,用于购买某件商品,贷款的月利率为5%(按复利计算),按照还款合同,马云同学每个月都还款x万元,20个月还清,则下列关系式正确的是( )
| A. | 20x=M | B. | 20x=M(1+5%)20 | C. | 20x<M(1+5%)20 | D. | 20x>M(1+5%)20 |
15.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )


| A. | 24π | B. | 12π | C. | 8π | D. | 6π |
2.在空间直角坐标系中,在z轴上的点的坐标可记为( )
| A. | (0,b,0) | B. | (a,0,0) | C. | (0,0,c) | D. | (0,b,c) |
12.已知各项均为正数的等比数列{an}满足a3•a5=64,a2=2,则a1=( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
19.下列函数中,既是偶函数又在(-∞,0)上单调递增的函数是( )
| A. | y=x2 | B. | y=ex | C. | y=log0.5|x| | D. | y=sinx |
16.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频数作为各需求量发生的概率.
(1)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;
(2)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?说明理由.
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(1)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;
(2)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?说明理由.
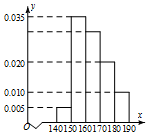 某高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若在身高[160,170),[170,180),[180,190]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[160,170)内的学生中选取的人数应为15.
某高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若在身高[160,170),[170,180),[180,190]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[160,170)内的学生中选取的人数应为15.