题目内容
已知f(x)=|sinx|(x≥0),y=g(x)是过原点且与y=f(x)图象恰有三个交点的直线,这三个交点的横坐标分别为0,α,β(0<α<β),那么下列结论中正确的有 .(填正确结论的序号)
①f(x)-g(x)≤0的解集为[α,+∞);
②y=f(x)-g(x)在(
,α)上单减;
③αsinβ+βsinα=0
④当x=π时,y=f(x)-g(x)取得最小值.
①f(x)-g(x)≤0的解集为[α,+∞);
②y=f(x)-g(x)在(
| π |
| 2 |
③αsinβ+βsinα=0
④当x=π时,y=f(x)-g(x)取得最小值.
考点:命题的真假判断与应用
专题:函数的性质及应用,三角函数的图像与性质
分析:画出f(x)=|sinx|(x≥0),的图象,过原点的直线与函数y=|sinx|(x≥0)的图象有且只有三个交点,则直线与函数y=|sinx|(x≥0)在区间(π,2π)内的图象相切,由图象可知,
<α<π,π<β<
,
故由题意设切点坐标为(β,-sinβ),运用导数,得β=tanβ.即直线y=-cosβ•x,
对于①,f(x)-g(x)≤0的解集,由图象可知;对于②,在(
,α)上,求出导数,即可判断;
对于③,由β=tanβ和sinα=-cosβ•α,即可判断;对于④,由②知,当x=α时,y=f(x)-g(x)取得最小值.
| π |
| 2 |
| 3π |
| 2 |
故由题意设切点坐标为(β,-sinβ),运用导数,得β=tanβ.即直线y=-cosβ•x,
对于①,f(x)-g(x)≤0的解集,由图象可知;对于②,在(
| π |
| 2 |
对于③,由β=tanβ和sinα=-cosβ•α,即可判断;对于④,由②知,当x=α时,y=f(x)-g(x)取得最小值.
解答:
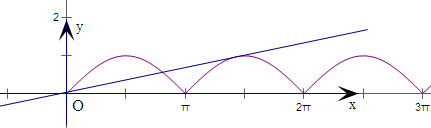 解:画出f(x)=|sinx|(x≥0),的图象,
解:画出f(x)=|sinx|(x≥0),的图象,
∵过原点的直线与函数y=|sinx|(x≥0)的图象有且只有三个交点,
∴直线与函数y=|sinx|(x≥0)在区间(π,2π)内的图象相切,
在区间(π,2π)上,f(x)的解析式为y=-sinx,且
<α<π,π<β<
,
故由题意设切点坐标为(β,-sinβ),∴切线斜率k=y′=-cosx|x=β=-cosβ,
∴由点斜式得切线方程为:y+sinβ=-cosβ(x-β),∴y=-cosβ•x+βcosβ-sinβ,
∵直线过原点,∴βcosβ-sinβ=0,得β=tanβ.即直线y=-cosβ•x,
对于①,f(x)-g(x)≤0的解集,由图象可知为[α,+∞),故①对;
对于②,在(
,α)上,y=sinx+cosβ•x,y′=cosx+cosβ<0,故②对;
对于③,由sinα=-cosβ•α,αsinβ+βsinα=αsinβ-αβcosβ=αsinβ-αtanβcosβ
=αsinβ-αsinβ=0,故③对;
对于④,由②知,当x=α时,y=f(x)-g(x)取得最小值,故④不正确.
故答案为:①②③.
 解:画出f(x)=|sinx|(x≥0),的图象,
解:画出f(x)=|sinx|(x≥0),的图象,∵过原点的直线与函数y=|sinx|(x≥0)的图象有且只有三个交点,
∴直线与函数y=|sinx|(x≥0)在区间(π,2π)内的图象相切,
在区间(π,2π)上,f(x)的解析式为y=-sinx,且
| π |
| 2 |
| 3π |
| 2 |
故由题意设切点坐标为(β,-sinβ),∴切线斜率k=y′=-cosx|x=β=-cosβ,
∴由点斜式得切线方程为:y+sinβ=-cosβ(x-β),∴y=-cosβ•x+βcosβ-sinβ,
∵直线过原点,∴βcosβ-sinβ=0,得β=tanβ.即直线y=-cosβ•x,
对于①,f(x)-g(x)≤0的解集,由图象可知为[α,+∞),故①对;
对于②,在(
| π |
| 2 |
对于③,由sinα=-cosβ•α,αsinβ+βsinα=αsinβ-αβcosβ=αsinβ-αtanβcosβ
=αsinβ-αsinβ=0,故③对;
对于④,由②知,当x=α时,y=f(x)-g(x)取得最小值,故④不正确.
故答案为:①②③.
点评:本题考查正弦函数的图象,考查导数知识的运用,考查学生分析解决问题的能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )
如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )A、14
| ||
B、6+2
| ||
C、12+2
| ||
D、16+2
|
若f(x)=|x+2|+|x-4|的最小值为( )
| A、6 | B、-6 | C、-2 | D、2 |
 如图所示是某几何体的三视图,其中正视图是斜边为2的直角三角形,侧视图是半径为1的半圆,则该几何体的体积是
如图所示是某几何体的三视图,其中正视图是斜边为2的直角三角形,侧视图是半径为1的半圆,则该几何体的体积是