如图.在四棱锥P﹣ABCD中.PD⊥平面ABCD.底面ABCD是菱形.∠BAD=60°.AB=2.PD=.O为AC与BD的交点.E为棱PB上一点．(Ⅰ)证明:平面EAC⊥平面PBD,(Ⅱ)若PD∥平面EAC.求三棱锥P﹣EAD的体积．题目和参考答案——青夏教育精英家教网—

题目内容

如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60°，AB=2，PD=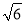，O为AC与BD的交点，E为棱PB上一点．

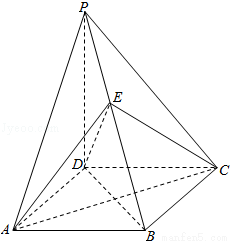
（Ⅰ）证明：平面EAC⊥平面PBD；

（Ⅱ）若PD∥平面EAC，求三棱锥P﹣EAD的体积．

练习册系列答案

浙江期末复习系列答案

相关题目

数列的前项和为.

（1）求的通项公式；

（2）问的前多少项和最大；

（3）设，求数列的前项和.

在等比数列所以中, , 则等于（）

A．或 B．或 C． D．

在正三棱锥P?ABC中，D，E分别是AB，BC的中点，下列结论：①AC⊥PB；②AC∥平面PDE；③AB⊥平面PDE，其中错误的结论个数是（）

A．0 B．1 C．2 D．3

在长方体中，AB＝BC＝2，，则与平面所成角的正弦值为（）

A． B． C． D．

已知a＞0，b∈R，函数f（x）=4ax2﹣2bx﹣a+b，x∈[0，1]．

（Ⅰ）当a=b=2时，求函数f（x）的最大值；

（Ⅱ）证明：函数f（x）的最大值|2a﹣b|+a；

（Ⅲ）证明：f（x）+|2a﹣b|+a≥0．

在平面上，若两个正三角形的边长之比1:2，则它们的面积之比为1:4，类似地，在空间中，若两个正四面体的棱长之比为1:2，则它的体积比为（）

A.1:4 B.1:6 C.1:8 D.1:9

已知函数．

（1）求及的单调递增区间；

（2）求在闭区间的最值．

从某地区一次中学生知识竞赛中, 随机抽取了名学生的成绩, 绘成如图所示的列联表（甲组优秀, 乙组一般）:

（1）试问有没有的把握认为成绩分在甲组或乙组与性别有关；

（2）①如果用分层抽样的方法从甲组和乙组中抽取人，再从人中随机抽取人，那么至少有人在甲组的概率是多少？

②用样本估计总体，把频率作为概率，若从该地区所有的中学（人数很多）中随机抽取人，用表示所选人中甲组的人数，试写出的分布列，并求出的数学期望.

，其中

独立性检验临界表:

试题分类