题目内容
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(![]() )①前
)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由.②通项公式为
是否是“回归数列”?并请说明理由.②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(![]() )设
)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值.
的值.
(![]() )是否对任意的等差数列
)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )见解析.
)见解析.
【解析】试题分析: ![]() 利用当
利用当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 即可得到
即可得到![]() ,再利用“回归数列”的意义即可得出;②
,再利用“回归数列”的意义即可得出;②![]() ,
, ![]() ,
, ![]() 为偶数,即可证明数列
为偶数,即可证明数列![]() 是“回归数列”
是“回归数列”
![]() 利用等差数列的前
利用等差数列的前![]() 项和即可得到
项和即可得到![]() ,对任意
,对任意![]() ,存在
,存在![]() ,使
,使![]() ,取
,取![]() 时和根据
时和根据![]() 即可得出结论
即可得出结论
![]() 设等差数列
设等差数列![]() 的公差为
的公差为![]() ,构造数列
,构造数列![]() ,
, ![]() ,可证明
,可证明![]() 和
和![]() 是等差数列。再利用等差数列的前
是等差数列。再利用等差数列的前![]() 项和公式及其通项公式,“回归数列”,即可得出;
项和公式及其通项公式,“回归数列”,即可得出;
解析:(![]() )①当
)①当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
∴数列![]() 是“回归数列”.
是“回归数列”.
②![]() ,前
,前![]() 项和
项和![]() ,
,
∵![]() 为偶数,
为偶数,
∴存在![]() ,
,
即![]() ,使
,使![]() ,
,
∴数列![]() 是“回归数列”.
是“回归数列”.
(![]() )
)![]() ,
,
对任意![]() ,存在
,存在![]() ,使
,使![]() ,
,
即![]() ,
,
取![]() 时,得
时,得![]() ,解得
,解得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )设等差数列
)设等差数列![]() 的公差为
的公差为![]() ,令
,令![]() ,
,
对![]() ,
, ![]() ,
,
令![]() ,则对
,则对![]() ,
, ![]() ,
,
则![]() ,且数列
,且数列![]() 和
和![]() 是等差数列,
是等差数列,
数列![]() 的前
的前![]() 项和
项和![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() 与
与![]() 的奇偶性不同,
的奇偶性不同,
故![]() 为非负偶数,
为非负偶数,
∴![]() ,
,
∴对![]() ,都可找到
,都可找到![]() ,使
,使![]() 成立,
成立,
即![]() 为“回归数列”.
为“回归数列”.
数列![]() 的前
的前![]() 项和
项和![]() ,
,
∴![]() ,
,
则![]() ,
,
∵对![]() ,
, ![]() 为非负偶数,
为非负偶数,
∴![]() ,
,
∴对![]() ,都可找到
,都可找到![]() ,使得
,使得![]() 成立,
成立,
即![]() 为“回归数列”,
为“回归数列”,
故命题得证.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 4 | 6 | 7 | 8 | 10 |
销量 | 60 | 50 | 45 | 30 | 20 |
(1) 请根据上表提供的数据画出散点图,并判断是正相关还是负相关;
(2) 求出![]() 关于
关于![]() 的回归直线方程,若单价为9元时,预测其销量为多少?
的回归直线方程,若单价为9元时,预测其销量为多少?
(参考公式:回归直线方程中公式 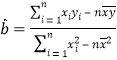 ,
,![]() )
)
【题目】下表数据为某地区某种农产品的年产量x(单位:吨)及对应销售价格y(单位:千元/吨) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y与x有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程.
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润Z最大?
(参考公式:回归直线方程为![]() ,
,![]() ,
,![]() )
)