题目内容
若z=sinθ-
+i(cosθ-
),z是纯虚数,则tan(θ-
)= .
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 4 |
考点:复数的基本概念
专题:数系的扩充和复数
分析:根据复数的概念即可得到结论.
解答:
解:∵z是纯虚数,
∴cosθ-
=0且sinθ-
≠0,
即cosθ=
且sinθ≠
,
则sinθ=-
,
故tan=-
,
则tan(θ-
)=
=
=-7,
故答案为:-7
∴cosθ-
| 4 |
| 5 |
| 3 |
| 5 |
即cosθ=
| 4 |
| 5 |
| 3 |
| 5 |
则sinθ=-
| 3 |
| 5 |
故tan=-
| 3 |
| 4 |
则tan(θ-
| π |
| 4 |
| tanθ-1 |
| 1+tanθ |
-
| ||
1-
|
故答案为:-7
点评:本题主要考查复数的有关概念以及两角和的正切公式的计算,比较基础.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
现从200件产品中随机出20件进行质量检验,列说法正确是( )
| A、200件产品是总体 |
| B、20件产品是样本 |
| C、样本容量是200 |
| D、样本容量是20 |
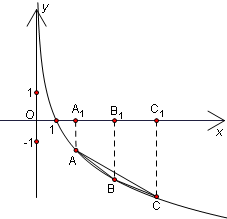 如图,A,B,C是函数
如图,A,B,C是函数