题目内容
已知数列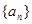 是等差数列,
是等差数列,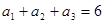 ,
,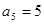 .
.
(Ⅰ)求数列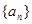 的通项公式;
的通项公式;
(Ⅱ)若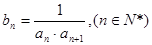 ,求数列
,求数列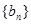 的前
的前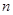 项和
项和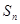 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)由两个已知条件分别列出关于首项和公差的一个二元一次方程组,从而解得首项和公差的值.再用等差数列的通项公式即可得结论.
(Ⅱ)由(Ⅰ)的通项代入即可求得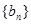 的通项公式,通项是一个通过裂项求差的形式.
的通项公式,通项是一个通过裂项求差的形式.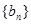 的前n项和通过累加即可剩下头尾两项的差.即可求得前n项和的结论.本题是一道较基础的等差数列问题的题目,通过求出首相和公差,再利用裂项求差的方法.
的前n项和通过累加即可剩下头尾两项的差.即可求得前n项和的结论.本题是一道较基础的等差数列问题的题目,通过求出首相和公差,再利用裂项求差的方法.
试题解析:(Ⅰ)设等差数列的公差为
∵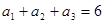 ,
,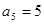
∴
解得:
∴ 
(Ⅱ)∵
∴

即数列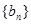 的前n项和
的前n项和
考点:1.等差数列的通项公式.2.裂项求和法.3.解方程的思想.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
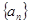 和等比数列
和等比数列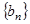 中,
中,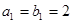 ,
,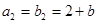 ,
,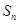 是
是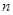 项和.
项和.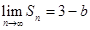 ,求实数
,求实数 的值;
的值;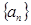 中?若存在,求出所有的
中?若存在,求出所有的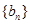 中至少有三项在数列
中至少有三项在数列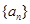 中,但
中,但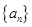 的前
的前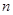 项和为
项和为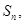 记
记
 的等差数列,求
的等差数列,求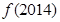 ;
;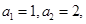 且数列
且数列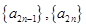 均是公比为
均是公比为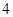 的等比数列,
的等比数列,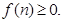
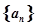 满足
满足 .
. 的前15项的和
的前15项的和 ;
; 满足
满足 ,
, ,求数列
,求数列 的前
的前 项的和
项的和
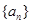 是公差大于零的等差数列,已知
是公差大于零的等差数列,已知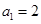 ,
,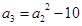 .
.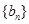 是以函数
是以函数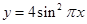 的最小正周期为首项,以
的最小正周期为首项,以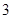 为公比的等比数列,求数列
为公比的等比数列,求数列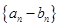 的前
的前 项和
项和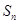 .
. 具有性质:①
具有性质:①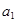 为正数;②对于任意的正整数
为正数;②对于任意的正整数 ,当
,当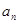 为偶数时,
为偶数时, ;当
;当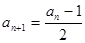
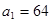 ,求数列
,求数列 成等差数列,求
成等差数列,求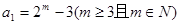 ,数列
,数列 ,求证:
,求证:
 为等比数列,
为等比数列,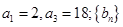 是等差数列,
是等差数列,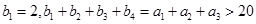
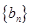 的通项公式及前
的通项公式及前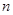 项和
项和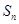 ;
;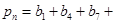
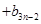 ,
,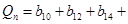
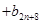 ,其中
,其中 ,试比较
,试比较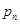 与
与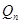 的大小,并加以证明.
的大小,并加以证明.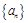 中,
中,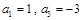 .
.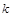 项和
项和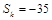 ,求
,求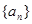 的前
的前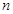 项的和为
项的和为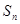 ,
, 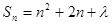 ,求证:数列
,求证:数列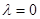 .
.