题目内容
已知对任意正整数n,满足fn+1(x)=fn′(x),且f1(x)=sinx,则f2013(x)=( )
| A.sinx | B.-sinx | C.cosx | D.-cosx |
由f1(x)=sinx,得f2(x)=f1′(x)=(sinx)′=cosx.
f3(x)=f2′(x)=(cosx)′=-sinx.
f4(x)=f3′(x)=(-sinx)′=-cosx.
f5(x)=f4′(x)=(-cosx)′=sinx.
…
由上可知,fn(x)呈周期出现,且4为周期.
由2013=4×503+1
所以f2013(x)=f4×503+1(x)=f1(x)=sinx.
故选A.
f3(x)=f2′(x)=(cosx)′=-sinx.
f4(x)=f3′(x)=(-sinx)′=-cosx.
f5(x)=f4′(x)=(-cosx)′=sinx.
…
由上可知,fn(x)呈周期出现,且4为周期.
由2013=4×503+1
所以f2013(x)=f4×503+1(x)=f1(x)=sinx.
故选A.

练习册系列答案
相关题目
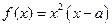 .
.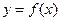 在点
在点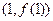 处的切线
处的切线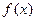 在区间[0,2]上的最大值。
在区间[0,2]上的最大值。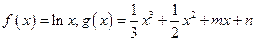 ,直线
,直线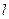 与函数
与函数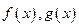 的图象都相切于点
的图象都相切于点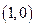 。
。 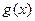 的解析式;
的解析式;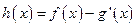 (其中
(其中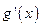 是
是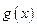 的导函数),求函数
的导函数),求函数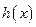 的极大值.
的极大值.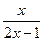 在点(1,1)处的切线方程为( )
在点(1,1)处的切线方程为( )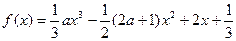 ,
,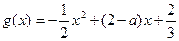
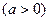 (Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,
(Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,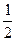 ]内至少存在一实数
]内至少存在一实数 x0使得
x0使得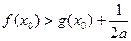 成立,求实数a的取值范围.
成立,求实数a的取值范围.