题目内容
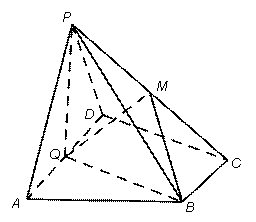
如图,在四棱锥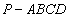 中,底面
中,底面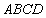 为直角梯形,
为直角梯形,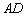 ∥
∥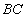 ,
,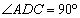 ,平面
,平面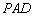 ⊥底面
⊥底面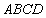 ,
,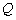 为
为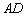 的中点,
的中点,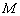 是棱
是棱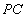 上的点,
上的点,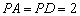 ,
,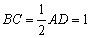 ,
,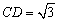 .
.
(1)求证:平面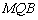 ⊥平面
⊥平面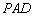 ;
;
(2)若满足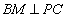 ,求异面直线
,求异面直线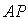 与
与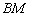 所成角的余弦值;
所成角的余弦值;
(3)若二面角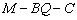 大小为60°,求
大小为60°,求 的长.
的长.
解答:(Ⅰ)∵AD // BC,BC=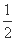 AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD // BQ .
∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
 ∵BQ
∵BQ 平面MQB,
平面MQB,
∴平面MQB⊥平面PAD.
(Ⅱ)∵PA=PD,Q为AD的中点,
∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且
平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
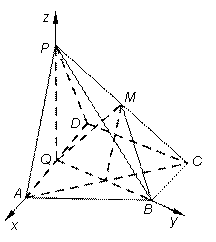
如图,以Q为原点建立空间直角坐标系.则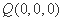 ,
,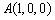 ,
,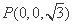 ,
,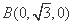 ,
,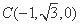
由 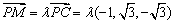 ,且
,且 ,得
,得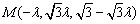
∵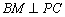 ,
,
∴ 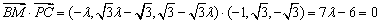 …………6分
…………6分
∴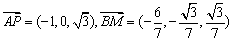
设异面直线AP与BM所成角为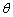
则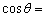
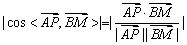 =
=
∴异面直线AP与BM所成角的余弦值为
(Ⅲ)由(Ⅱ)知平面BQC的法向量为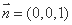
由 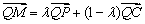 ,且
,且 ,得
,得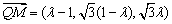
又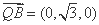 ,
,
∴ 平面MBQ法向量为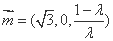 .
.
∵二面角M-BQ-C为30°, ∴ ,
,
∴ 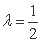 .∴
.∴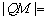

练习册系列答案
相关题目

 都有
都有 ”的否定是
”的否定是  满足
满足 ,则
,则 的最小值是
的最小值是 .
.
 .
.
 .
.
 .
.
 是双曲线
是双曲线 的左、右焦点,若点
的左、右焦点,若点 关于直线
关于直线 的对称点
的对称点 也在双曲线上,则该双曲线的离心率为__ _.
也在双曲线上,则该双曲线的离心率为__ _. 的导数是 ( )
的导数是 ( ) B.
B. C.
C. D.
D.
 的展开式的常数项为第( )项
的展开式的常数项为第( )项 则z=5y-x的最大值是( )
则z=5y-x的最大值是( )