题目内容
设函数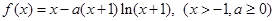 .
.
(1)求 的单调区间;
的单调区间;
(2)当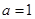 时,若方程
时,若方程 在
在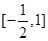 上有两个实数解,求实数
上有两个实数解,求实数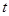 的取值范围;
的取值范围;
(3)证明:当 时,
时,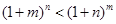 .
.
(1)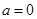 时,在
时,在 上是增函数;
上是增函数;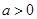 时,在
时,在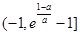 上单调递增,在
上单调递增,在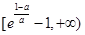 上单调递减.(2)
上单调递减.(2)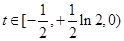 ,(3)详见解析
,(3)详见解析
解析试题分析:(1)求函数单调区间,首先明确定义域,再求导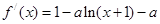 ,由于含有参数,需分类讨论根的情况.
,由于含有参数,需分类讨论根的情况. 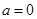 时,
时,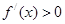 ,所以
,所以 在
在 上是增函数.当
上是增函数.当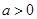 时,由
时,由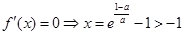 ,所以
,所以 在
在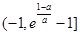 上单调递增,在
上单调递增,在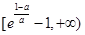 上单调递减.(2)本题考查函数与方程思想,实际研究直线
上单调递减.(2)本题考查函数与方程思想,实际研究直线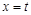 与函数
与函数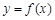 图像交点有两个的情况,由(1)知
图像交点有两个的情况,由(1)知 在
在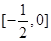 上单调递增,在
上单调递增,在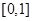 上单调递减,且
上单调递减,且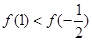 ,所以当
,所以当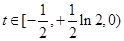 时,方程
时,方程 有两解.(3)本题关键在于构造函数,首先将两变量分离,这要用到取对数,即
有两解.(3)本题关键在于构造函数,首先将两变量分离,这要用到取对数,即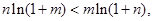 因此只需证
因此只需证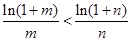 ,即证
,即证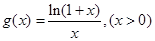 为单调减函数,可利用导数
为单调减函数,可利用导数 ,再结合(1)的结论,可证.
,再结合(1)的结论,可证.
试题解析:(1)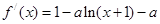 .
.
①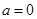 时,
时,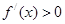 ,∴
,∴ 在
在 上是增函数. 1分
上是增函数. 1分
②当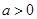 时,由
时,由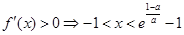 ,由
,由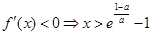 ,
,
∴ 在
在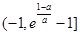 上单调递增,在
上单调递增,在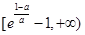 上单调递减. 4分
上单调递减. 4分
(2)当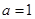 时,由(1)知,
时,由(1)知, 在
在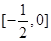 上单调递增,在
上单调递增,在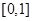 上单调递减,
上单调递减,
又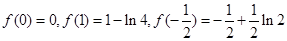 , 6分
, 6分
∴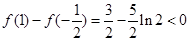 .
.
∴当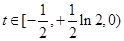 时,方程
时,方程 有两解. 8分
有两解. 8分
(3)∵ .∴要证:
.∴要证: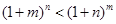 只需证
只需证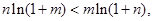
只需证: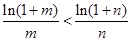 .
.
设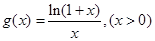 , 10分
, 10分
则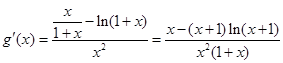 .
.
由(1)知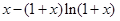 在
在 单调递减, 12分
单调递减, 12分
∴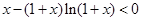 ,即
,即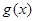 是减函数,而
是减函数,而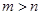 .
.
∴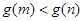 ,故原不等式成立. 14分
,故原不等式成立. 14分
考点:利用导数求单调区间,利用导数证不等式

练习册系列答案
相关题目
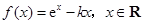
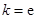 ,试确定函数
,试确定函数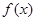 的单调区间;
的单调区间;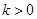 ,且对于任意
,且对于任意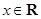 ,
,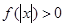 恒成立,试确定实数
恒成立,试确定实数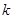 的取值范围;
的取值范围;
 .
.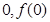 )处的切线方程;
)处的切线方程;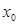 使得
使得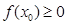 ,求
,求 的取值范围.
的取值范围. .
. 的单调区间;
的单调区间; 时,求证:
时,求证: 恒成立..
恒成立..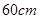 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?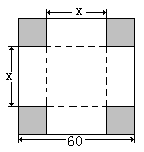
 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;  求函数
求函数 的单调区间.
的单调区间. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 上为减函数,求实数
上为减函数,求实数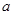 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 在
在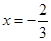 与
与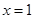 时都取得极值.
时都取得极值.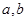 的值;
的值;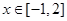 ,不等式
,不等式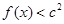 恒成立,求
恒成立,求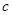 的取值范围.
的取值范围.