题目内容
已]知f(x)=x|x-a|-2.
(1)当a=1时,解f(x)<|x-2|;
(2)当x∈(0,1)时,f(x)<x2-1恒成立,求a的取值范围.
(1)当a=1时,解f(x)<|x-2|;
(2)当x∈(0,1)时,f(x)<x2-1恒成立,求a的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:计算题,分类讨论,函数的性质及应用,不等式的解法及应用
分析:(1)利用a=1,化简不等式,通过x≥2,1≤x<2,x<1分别去掉绝对值符号,然后求解不等式即可.
(2)当x∈(0,1]时,f(x)<x2-1恒成立,转化为a的表达式,通过函数的单调性以及基本不等式求出表达式的最值,得到a的范围.
(2)当x∈(0,1]时,f(x)<x2-1恒成立,转化为a的表达式,通过函数的单调性以及基本不等式求出表达式的最值,得到a的范围.
解答:
解:(1)a=1,f(x)<|x-2|即为x|x-1|-2<|x-2|.
①当x≥2时,上式化为x(x-1)-2<x-2,又x≥2,∴x∈∅;
②当1≤x<2时,由x|x-1|-2<|x-2|,可得x(x-1)-2<2-x,解得-2<x<2,
又1≤x<2,∴1≤x<2;
③当x<1时,x|x-1|-2<|x-2|可得x(1-x)-2<2-x,解得x<1;
综上不等式的解集为{x|x<2}.
(2)当x∈(0,1]时,f(x)<x2-1即x|x-a|-2<x2-1恒成立,
即|x-a|<x+
,即有-
<a<2x+
在x∈(0,1]上恒成立.
而g(x)=-
在(0,1]上为增函数,所以g(x)max=g(1)=-1..
h(x)=2x+
≥2
=2
.当且仅当2x=
,即x=
取等号.
即有a的取值范围为-1<a<2
.
①当x≥2时,上式化为x(x-1)-2<x-2,又x≥2,∴x∈∅;
②当1≤x<2时,由x|x-1|-2<|x-2|,可得x(x-1)-2<2-x,解得-2<x<2,
又1≤x<2,∴1≤x<2;
③当x<1时,x|x-1|-2<|x-2|可得x(1-x)-2<2-x,解得x<1;
综上不等式的解集为{x|x<2}.
(2)当x∈(0,1]时,f(x)<x2-1即x|x-a|-2<x2-1恒成立,
即|x-a|<x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
而g(x)=-
| 1 |
| x |
h(x)=2x+
| 1 |
| x |
2x•
|
| 2 |
| 1 |
| x |
| ||
| 2 |
即有a的取值范围为-1<a<2
| 2 |
点评:本题考查绝对值不等式,函数的恒成立问题注意运用参数分离,转化为求函数的最值,考查函数的单调性,分类讨论思想,属于中档题和易错题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
设点(3,4)为偶函数y=f(x)图象上的点,则下列各点在函数图象上的是( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-3,-4) |
| D、(-4,-3) |
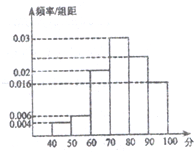 从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.
从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.