题目内容
20. 如图,已知四棱锥P-ABCD的底面是菱形,PB=PD,E为PA的中点.
如图,已知四棱锥P-ABCD的底面是菱形,PB=PD,E为PA的中点.(1)求证:PC∥平面BDE;
(2)求证:平面PAC⊥平面BDE;
(3)若∠DAB=60°,BP=BD=PC,求BP与平面ABCD所成角的正弦值.
分析 (1)通过连接底面的对角线,进一步利用三角形的中位线,把线线平行转化成线面平行.
(2)进一步根据线线垂直转化成线面垂直,转化成面面垂直.
(3)利用棱锥的棱长关系式,得到三棱锥P-BDC为正三棱锥,进一步求出线面的夹角,最后转化出结果.
解答 证明:(1)连接AC,交BD于点O,连接OE,
已知四棱锥P-ABCD的底面是菱形,E为PA的中点.
所以:O为AC的中点,
所以:在△APC中,OE∥PC.
OE?平面BDE,CP?平面BDE,
所以:PC∥平面BDE.
(2)由于底面ABCD是菱形,
所以:AC⊥BD,
又BP=DP,
所以:△DBP是等腰三角形.
PO⊥BD,
则:BD⊥平面PAC,
BD?平面BDE,
则:平面PAC⊥平面BDE.
(3)在底面中,∠DAB=60°,
所以:△BDC为等边三角形.
又BP=BD=PC,
所以:三棱锥P-BDC为正三棱锥.
设:棱长为x,
则:BD=BC=DC=PD=PB=PC=x,
点P在下底面的射影为△BDC的中心F.
进一步求得:BF=$\frac{\sqrt{3}}{3}x$,
由于:PF⊥底面ABCD,
所以:∠PBF为BP与底面ABCD的夹角.
则:cos∠PBF=$\frac{PF}{BP}$=$\frac{\sqrt{3}}{3}$.
所以:sin∠PBF=$\frac{\sqrt{6}}{3}$.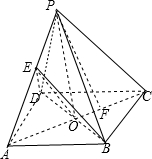
点评 本题考查的知识要点:线面平行的判定定理,线面垂直的判定定理和面面垂直的判定定理,线面的夹角及相关的运算问题.

练习册系列答案
相关题目
10.把等腰直角△ABC沿斜边上的高AD折成直二面角B-AD-C,则BD与平面ABC所成角的正切值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
11.已知线段BC为斜线段AB在平面α内的射影,BD?α,若∠ABD=60°,∠CBD=45°,则AB和平面α所成的角为( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
 如图,在直三棱锥ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点且B1M与平面ACC1所成角为30°,确定M的位置.
如图,在直三棱锥ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点且B1M与平面ACC1所成角为30°,确定M的位置.