题目内容
一个无穷等比数列的公比q适合0<q<1,且它的第4项与第8项之和等于
,而第5项与第7项之积等于
,则这个无穷等比数列各项的和是( )
| 17 |
| 8 |
| 1 |
| 4 |
| A、32 | B、4 | C、8 | D、16 |
分析:由题意可列方程组解得此数列,再利用无穷等比数列各项和公式得解.
解答:解:设首项a1公比q,则得方程组
,
从而解得:a4=2,a8=
.又∵a8=a4×q4,
∴q=
,易得a1=16
由无穷等比数列的公比0<q<1,可知无穷等比数列各项的和S=
=
=32
故选A.
|
从而解得:a4=2,a8=
| 1 |
| 8 |
∴q=
| 1 |
| 2 |
由无穷等比数列的公比0<q<1,可知无穷等比数列各项的和S=
| a1 |
| 1-q |
| 16 | ||
1--
|
故选A.
点评:本题考查等比数列的性质及无穷递缩等比数列各项和的求法.要注意无穷递缩等比数列各项和的求法.

练习册系列答案
相关题目
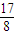 ,而第5项与第7项之积等于
,而第5项与第7项之积等于 ,则这个无穷等比数列各项的和是( )
,则这个无穷等比数列各项的和是( )