题目内容
【题目】某公司为了激励业务员的积极性,对业绩在60万到200万的业务员进行奖励奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元同时奖金不超过业绩值的5%.
(1)若某业务员的业绩为100万核定可得4万元奖金,若该公司用函数![]() (k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知
(k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知![]() ,
,![]() )
)
(2)若采用函数![]() 作为奖励函数模型试确定最小的正整数a的值.
作为奖励函数模型试确定最小的正整数a的值.
【答案】(1)![]() 万元;(2)481
万元;(2)481
【解析】
(1)将![]() ,
,![]() 代入求出参数
代入求出参数![]() 的值,即可求出函数解析式,再将
的值,即可求出函数解析式,再将![]() 代入求值即可;
代入求值即可;
(2)根据所给函数模型![]() ,函数在
,函数在![]() 上单调递增,所以
上单调递增,所以![]() ,且
,且![]() 即可求出参数
即可求出参数![]() 取值范围,从而得到最小正整数
取值范围,从而得到最小正整数![]() 的值.
的值.
解:(1)对于函数模型![]() (
(![]() 为常数),
为常数),
当![]() 时,
时,![]() ,代入解得
,代入解得![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,∴业绩200万元的业务员可以得到
,∴业绩200万元的业务员可以得到![]() 万元奖励.
万元奖励.
(2)对于函数模型![]() .
.
因为![]() 为正整数,所以函数在
为正整数,所以函数在![]() 递增;
递增;![]() ,解得
,解得![]() ;
;
要使![]() 对
对![]() 成立,即
成立,即![]() 对
对![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 上的最大值为480.2,所以
上的最大值为480.2,所以![]() .综上可知
.综上可知![]() ,
,
即满足条件的最小正整数![]() 的值为481.
的值为481.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某市工业部门计划对所辖中小型企业推行节能降耗技术改造,下面是对所辖企业是否支持技术改造进行的问卷调查的结果:
支持 | 不支持 | 合计 | |
中型企业 | 40 | ||
小型企业 | 240 | ||
合计 | 560 |
已知从这560家企业中随机抽取1家,抽到支持技术改造的企业的概率为![]() .
.
(1)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(2)从上述支持节能降耗的中小企业中按分层抽样的方法抽出12家企业,然后从这12家企业选出9家进行奖励,分别奖励中型企业50万元,小型企业10万元.设![]() 为所发奖励的金额.
为所发奖励的金额.
求![]() 的分布列和期望.
的分布列和期望.
附:![]()
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 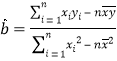 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
【题目】下列说法中,错误的是( )
A.将一组数据中的每个数据都加上同一个常数后,方差不变
B.对于回归方程![]() ,变量
,变量![]() 每增加一个单位,
每增加一个单位,![]() 平均增加5个单位
平均增加5个单位
C.线性回归方程![]() 所对应的直线必过点
所对应的直线必过点![]()
D.在一个![]() 列联表中,由计算得
列联表中,由计算得![]() ,则有
,则有![]() 的把握说两个变量有关
的把握说两个变量有关
本题可以参考独立性检验临界值表
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |