题目内容
15．已知函数f（x）=x2+bx+c，且f（-1）=f（3），则（ ）| A． | f（1）＜f（-1）＜c | B． | f（-1）＜c＜f（1） | C． | f（1）＜c＜f（3） | D． | c＜f（3）＜f（1） |
分析 由已知可得函数图象是开口朝上，且以直线x=1为对称轴的抛物线，结合函数的单调性和对称性，可得答案．
解答 解：∵函数f（x）=x2+bx+c，且f（-1）=f（3），
故函数图象是开口朝上，且以直线x=$\frac{-1+3}{2}$=1为对称轴的抛物线，
故函数f（x）=x2+bx+c在（-∞，1]上为减函数，
故f（3）=f（-1）＞f（0）＞f（1），
即f（1）＜c＜f（3），
故选：C．
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
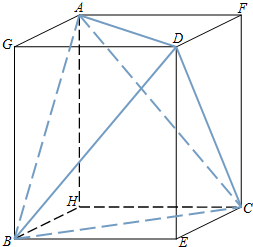如图，长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD．