题目内容
为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a( )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: 取1.4).
取1.4).
 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(
 )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: 取1.4).
取1.4).(1)可达8天;(2)a的最小值为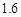 .
.
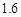 .
.试题分析:(1)根据题中条件每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间
 (单位:天)变化的函数关系已经给出,则易得一次喷洒4个单位的净化剂时的函数关系式:
(单位:天)变化的函数关系已经给出,则易得一次喷洒4个单位的净化剂时的函数关系式: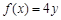 ,这样就得到一个分段函数,对分段函数的处理常用的原则:先分开,现合并,解两个不等式即可求解; (2)中若第一次喷洒2个单位的净化剂,6天后再喷洒a(
,这样就得到一个分段函数,对分段函数的处理常用的原则:先分开,现合并,解两个不等式即可求解; (2)中若第一次喷洒2个单位的净化剂,6天后再喷洒a( )个单位的药剂,根据题意从第6天开始浓度来源与两方面,这是题中的难点,前面留下的为:
)个单位的药剂,根据题意从第6天开始浓度来源与两方面,这是题中的难点,前面留下的为: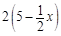 ,后面新增的为:
,后面新增的为: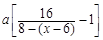 ,所得化简即可得到:
,所得化简即可得到: ,结合基本不等式知识求出最小值
,结合基本不等式知识求出最小值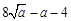 ,最后解一个不等式:
,最后解一个不等式: ,即可求解.
,即可求解.试题解析:(1)因为一次喷洒4个单位的净化剂,
所以浓度

则当
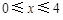 时,由
时,由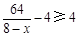 ,解得
,解得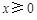 ,所以此时
,所以此时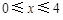 . 3分
. 3分当
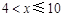 时,由
时,由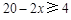 解得
解得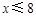 ,所以此时
,所以此时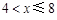 .
.综合得
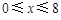 ,若一次投放4个单位的制剂,则有效净化时间可达8天. 7分
,若一次投放4个单位的制剂,则有效净化时间可达8天. 7分(2)设从第一次喷洒起,经x(
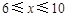 )天,
)天,浓度
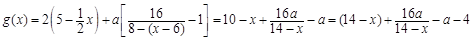 . 10分
. 10分因为
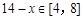 ,而
,而 ,
,所以
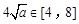 ,故当且仅当
,故当且仅当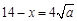 时,y有最小值为
时,y有最小值为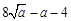 .
.令
 ,解得
,解得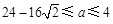 ,所以a的最小值为
,所以a的最小值为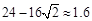 . 14分
. 14分
练习册系列答案
相关题目

 ,其中
,其中 ,
, 为正整数,
为正整数,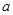 ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
. 的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底) 是实数,函数
是实数,函数 (
( ).
). 不是奇函数;
不是奇函数; 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的值域(用
的值域(用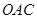 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域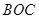 内,乙中转站建在区域
内,乙中转站建在区域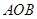 内.分界线
内.分界线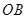 固定,且
固定,且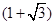 百米,边界线
百米,边界线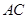 始终过点
始终过点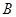 ,边界线
,边界线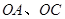 满足
满足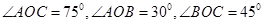 .
. (
(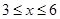 )百米,
)百米,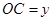 百米.
百米.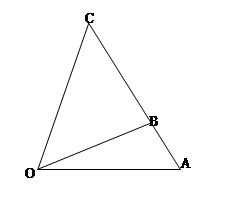
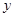 表示成
表示成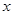 的函数,并求出函数
的函数,并求出函数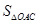 最小,并求出其面积的最小值.
最小,并求出其面积的最小值. .
. ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点; ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围.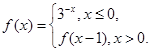 若
若 有且仅有三个解,则实数
有且仅有三个解,则实数 的取值范围是
的取值范围是 上的函数
上的函数 是最小正周期为
是最小正周期为 的偶函数,
的偶函数, 是
是 时;
时; ;当
;当 且
且 时,
时, ,则函数
,则函数 在区间
在区间 上的零点个数为( )
上的零点个数为( )
 ,则
,则 .
.