题目内容
求值:
(1)(
)-
-(
)0.5+(0.008)-
×
;
(2)2(lg
)2+lg
•lg5+
.
(1)(
| 27 |
| 8 |
| 2 |
| 3 |
| 49 |
| 9 |
| 2 |
| 3 |
| 2 |
| 25 |
(2)2(lg
| 2 |
| 2 |
(lg
|
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:计算题
分析:有指数的运算性质和对数的运算性质计算可得.
解答:
解:(1)原式=(
)
-(
)
+(
)
×
=
-
+25×
=-
+2
=
(2)原式=lg
(2lg
+lg5)+(1-lg
) (8分)
=lg
lg10+1-lg
=1 (10分)
| 8 |
| 27 |
| 2 |
| 3 |
| 49 |
| 9 |
| 1 |
| 2 |
| 1000 |
| 8 |
| 2 |
| 3 |
| 2 |
| 25 |
=
| 4 |
| 9 |
| 7 |
| 3 |
| 2 |
| 25 |
=-
| 17 |
| 9 |
=
| 1 |
| 9 |
(2)原式=lg
| 2 |
| 2 |
| 2 |
=lg
| 2 |
| 2 |
=1 (10分)
点评:本题主要考查指数的运算性质和对数的运算性质.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设0<b<a<1,则下列不等式成立的是( )
| A、ab<b2<1 |
| B、a2<b2 |
| C、2b<2a<2 |
| D、a2<ab<1 |
已知直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,若l1∥l2,则实数m的值是( )
| A、3 | B、-1,3 | C、-1 | D、-3 |
 如图,正方形ABCD是由四个全等的小直角三角形与中间的一个小正方形拼接而成,现随机地向大正方形内部区域投掷小球,若直角三角形的两条直角边的比是2:1,则小球落在小正方形区域的概率是( )
如图,正方形ABCD是由四个全等的小直角三角形与中间的一个小正方形拼接而成,现随机地向大正方形内部区域投掷小球,若直角三角形的两条直角边的比是2:1,则小球落在小正方形区域的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
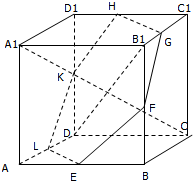 如图所示,正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求证:A1C⊥平面EFGHKL.
如图所示,正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求证:A1C⊥平面EFGHKL.