题目内容
如图J124所示,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
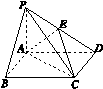
图J124
解:方法一:
(1)证明:∵PA⊥平面ABCD,CD⊂平面ABCD,
∴PA⊥CD.
又∵四边形ABCD是矩形,∴AD⊥CD.
又PA∩AD=A,PA,AD⊂平面PAD,∴CD⊥平面PAD.
又∵CD⊂平面PDC,∴平面PDC⊥平面PAD.
(2)取AD的中点O,连接EO,则EO∥PA.
∵PA⊥平面ABCD,∴EO⊥平面ABCD.
过点O作OF⊥AC交AC于点F,连接EF,
则∠EFO就是二面角EACD的平面角.
由PA=2,得EO=1.
在Rt△ADC中,由AD·CD=AC·h,得h=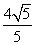 .
.
又∵O是AD的中点,OF⊥AC,∴OF=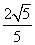 .
.
而EO=1,由勾股定理可得EF=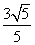 ,
,
故cos∠EFO=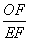 =
=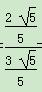 =
=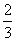 ,即二面角E AC D的余弦值为
,即二面角E AC D的余弦值为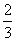 .
.

(3)延长AE,过点D作DG垂直AE于点G,连接CG.
由(1)可知,CD⊥AE,又CD∩DG=D,∴AE⊥平面CDG.
过点D作DH垂直CG于点H,则AE⊥DH.
又CG∩AE=G,∴DH⊥平面AGC,即DH⊥平面AEC,
∴CD在平面ACE内的射影是CH,
∴∠DCH是直线CD与平面AEC所成的角.
∵DG=AD·sin∠DAG=AD·sin∠OAE=AD·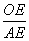 =
=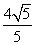 ,
,
又在Rt△CDG中,CD=2,∴CG=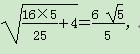
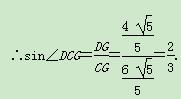
方法二:如图,以为A原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),E(0,2,1),P(0,0,2),
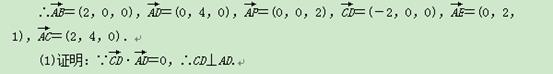
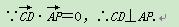
又∵AP∩AD=A,∴CD⊥平面PAD.
又∵CD⊂平面PDC,∴平面PDC⊥平面PAD.
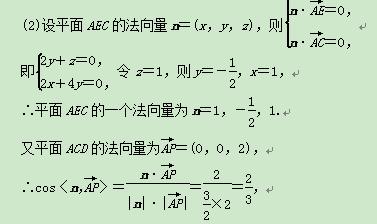 ∴二面角EACD的余弦值是
∴二面角EACD的余弦值是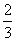 .
.
(3)设直线CD与平面AEC所成的角为θ.
∵平面AEC的一个法向量为n=1,- ,1,
,1,
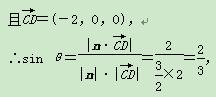 即直线CD与平面AEC所成角的正弦值为
即直线CD与平面AEC所成角的正弦值为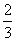 .
.

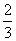 ,乙获胜的概率为
,乙获胜的概率为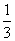 ,各局比赛结果相互独立.
,各局比赛结果相互独立. 的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )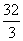 B.4π C.2π D.
B.4π C.2π D.
 B.
B.
 D.
D.
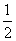
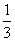 D.
D.
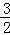 ,b=3 B. k=﹣
,b=3 B. k=﹣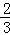 ,b=﹣3 C. k=﹣
,b=﹣3 C. k=﹣