题目内容
甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为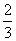 ,乙获胜的概率为
,乙获胜的概率为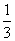 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
解 用A表示“甲在4局以内(含4局)赢得比赛”,Ak表示“第k局甲获胜”,Bk表示“第k局乙获胜”,则P(Ak)=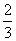 ,P(Bk)=
,P(Bk)=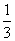 ,k=1,2,3,4,5.
,k=1,2,3,4,5.
(1)P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)
=P(A1)P(A2)+P(B1)P(A2)P(A3)+P(A1)P(B2)·P(A3)P(A4)
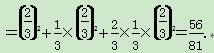 (2)X的可能取值为2,3,4,5.
(2)X的可能取值为2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)=P(A1)P(A2)+P(B1)P(B2)=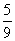 ,
,
P(X=3)=P(B1A2A3)+P(A1B2B3)
=P(B1)P(A2)P(A3)+P(A1)P(B2)P(B3)= ,
,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)
=P(A1)P(B2)P(A3)P(A4)
+P(B1)P(A2)P(B3)·P(B4)=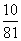 .
.
P(X=5)=1-P(X=2)-P(X=3)-P(X=4)=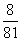 .
.
故X的分布列为
| X | 2 | 3 | 4 | 5 |
| P |
|
|
|
|

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 B.
B.
 D.
D.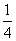

 B.8+
B.8+