题目内容
(12分)已知向量 ,
, ,
, ,
, .
.
(1)当 时,求向量
时,求向量 与
与 的夹角
的夹角 ;
;
(2)当 时,求
时,求 的最大值;
的最大值;
(3)设函数 ,将函数
,将函数 的图像向右平移s个长度单位,向上平移t个长度单位
的图像向右平移s个长度单位,向上平移t个长度单位 后得到函数
后得到函数 的图像,且
的图像,且 ,令
,令 ,求
,求 的最小值.
的最小值.
(1) ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)先确定当 时的
时的 、
、 ,再根据向量的数量积的坐标表示及模的表示确定
,再根据向量的数量积的坐标表示及模的表示确定 、
、 、
、 的模,然后根据
的模,然后根据 求出
求出 ;(2)利用二倍角公式及三角恒等变化表示出
;(2)利用二倍角公式及三角恒等变化表示出 =
= ,通过
,通过 ,确定出
,确定出 ,通过分析得知当
,通过分析得知当 ,
, 有最大值;(3)利用二倍角公式及三角恒等变化表示出
有最大值;(3)利用二倍角公式及三角恒等变化表示出 ,再根据图像平移“左加右减、上加下减”得到
,再根据图像平移“左加右减、上加下减”得到 ,
,  ,进而求
,进而求 的最小值.
的最小值.
试题解析:(1) ,
, ,
, 
而
 ,即
,即 .
.
(2)


 当
当 ,即
,即 ,
, .
.
(3)






 时,
时, .
.
考点:1、向量的数量积;2、三角恒等变换;3、最值问题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 中,
中, ,前
,前 项之和
项之和 ,则公比
,则公比 的值为( )
的值为( ) (B)
(B) (C)
(C) 或
或 (D)
(D) 或
或
 B.
B.
 D.
D.
 的定义域为R,当
的定义域为R,当 时,
时, 是增函数,则
是增函数,则 ,
, ,
, 的大小关系是( )
的大小关系是( ) B.
B.
 D.
D.
 上是增函数的是( )
上是增函数的是( )



 在A点处与圆 O相切,点P是圆O上的一个动点,且点P与点A不重合,则
在A点处与圆 O相切,点P是圆O上的一个动点,且点P与点A不重合,则 的取值范围是__________.
的取值范围是__________. 满足
满足 ,则
,则
 C.1 D.
C.1 D.
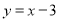 与抛物线
与抛物线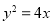 交于A、B两点,过A、B两点向抛物线的准线
交于A、B两点,过A、B两点向抛物线的准线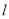 作垂线,垂足分别为P、Q,则梯形APQB的面积为
作垂线,垂足分别为P、Q,则梯形APQB的面积为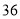 B.
B.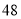 C.
C.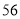 D.
D.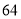
 与曲线
与曲线 有相同的( )
有相同的( )