题目内容
计算机考试分理论考试与上机操作考试两部分进行，每部分考试成绩只记“合格”与“不合格”，两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”．甲、乙、丙三人在理论考试中合格的概率分别为| 3 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 9 |
| 10 |
| 5 |
| 6 |
| 7 |
| 8 |
（1）甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大？
（2）求这三人计算机考试都获得“合格证书”的概率；
（3）用ξ表示甲、乙、丙三人在理论考核中合格人数，求ξ的分布列和数学期望Eξ．
分析：（1）对每个人，理论考试与上机操作考试都合格，才能获得“合格证书”，计算出每个人获得“合格证书”的概率，
进行比较．
（2）这三人计算机考试都获得“合格证书”的概率，等于每个人获得“合格证书”的概率之积．
（3）用ξ表示甲、乙、丙三人在理论考核中合格人数，则ξ可以取0，1，2，3，
再求出ξ取每个值时的概率，即得ξ的分布列，代入ξ的数学期望公式进行运算．
进行比较．
（2）这三人计算机考试都获得“合格证书”的概率，等于每个人获得“合格证书”的概率之积．
（3）用ξ表示甲、乙、丙三人在理论考核中合格人数，则ξ可以取0，1，2，3，
再求出ξ取每个值时的概率，即得ξ的分布列，代入ξ的数学期望公式进行运算．
解答：解：记“甲理论考试合格”为事件A1，“乙理论考试合格”为事件A2，“丙理论考试合格”为事件A3，记
为Ai的对立事件，i=1，2，3；记“甲上机考试合格”为事件B1，“乙上机考试合格”为事件B2，“丙上机考试合格”为事件B3．
（1）记“甲计算机考试获得合格证书”为事件A，记“乙计算机考试获得合格证书”为事件B，记“丙计算机考试获得合格证书”为事件C，则P(A)=
×
=
，P(B)=
×
=
，P(C)=
×
=
，
有P（B）＞P（C）＞P（A），
故乙获得“合格证书”可能性最大；（3分）
（2）记“三人该课程考核都合格”为事件D．
P（D）=P[（A1•B1）•（A2•B2）•（A3•B3）]
=P（A1•B1）•P（A2•B2）•P（A3•B3）
=P（A1）•P（B1）•P（A2）•P（B2）•P（A3）•P（B3）
=
×
×
×
×
×
．
=
，
所以，这三人该课程考核都合格的概率为
．（7分）
（3）用ξ表示甲、乙、丙三人在理论考核中合格人数，则ξ可以取0，1，2，3，
故ξ的分布列如下：
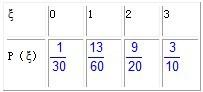（10分）
ξ的数学期望：Eξ=0×
+1×
+2×
+3×
=2
（12分）
. |
| Ai |
（1）记“甲计算机考试获得合格证书”为事件A，记“乙计算机考试获得合格证书”为事件B，记“丙计算机考试获得合格证书”为事件C，则P(A)=
| 3 |
| 5 |
| 9 |
| 10 |
| 27 |
| 50 |
| 3 |
| 4 |
| 5 |
| 6 |
| 5 |
| 8 |
| 2 |
| 3 |
| 7 |
| 8 |
| 7 |
| 12 |
有P（B）＞P（C）＞P（A），
故乙获得“合格证书”可能性最大；（3分）
（2）记“三人该课程考核都合格”为事件D．
P（D）=P[（A1•B1）•（A2•B2）•（A3•B3）]
=P（A1•B1）•P（A2•B2）•P（A3•B3）
=P（A1）•P（B1）•P（A2）•P（B2）•P（A3）•P（B3）
=
| 3 |
| 5 |
| 9 |
| 10 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2 |
| 3 |
| 7 |
| 8 |
=
| 63 |
| 320 |
所以，这三人该课程考核都合格的概率为
| 63 |
| 320 |
（3）用ξ表示甲、乙、丙三人在理论考核中合格人数，则ξ可以取0，1，2，3，
故ξ的分布列如下：
（10分）ξ的数学期望：Eξ=0×
| 1 |
| 30 |
| 13 |
| 60 |
| 9 |
| 20 |
| 3 |
| 10 |
| 1 |
| 60 |
点评：本题考查独立事件的概率的求法，以及离散型随机变量的分布列和数学期望的求法，关键在于求出随机变量取每个值时的概率．
练习册系列答案
名校课堂系列答案
相关题目
、
、
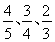
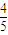，在实际操作考试中“合格”的概率依次为：
、
、
，所有考试是否合格相互之间没有影响．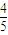
、
、
，在实际操作考试中“合格”的概率依次为：
、
、
，所有考试是否合格相互之间没有影响．