题目内容
已知函数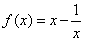
(1)判断函数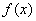 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数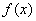 在区间
在区间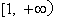 上为增函数;
上为增函数;
(3)若函数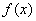 在区间
在区间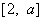 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于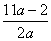 ,求
,求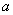 的取值范围.
的取值范围.
(1)解:函数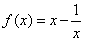 是奇函数.
是奇函数.
∵函数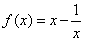 的定义域为
的定义域为 ,在
,在 轴上关于原点对称,
轴上关于原点对称,
且
∴函数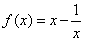 是奇函数.
是奇函数.
(2)证明:设任意实数
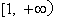 ,且
,且
则
∵ ∴
∴
∴ <0
<0
∴ <0 , 即
<0 , 即
∴函数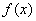 在区间
在区间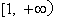 上为增函数.
上为增函数.
(3)解: ∵
∴函数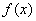 在区间
在区间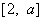 上也为增函数.
上也为增函数.
∴
若函数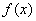 在区间
在区间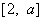 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于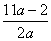 ,
,
则
∴
∴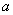 的取值范围是[4,+∞).
的取值范围是[4,+∞).

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 y的焦点F到其准线l的距离是( )
y的焦点F到其准线l的距离是( )
 i=i-1,则z =________.
i=i-1,则z =________. 若
若 ,则
,则 ( )
( ) B.
B. C.
C.
 是它的子集,
是它的子集, ;②若
;②若 =B,求
=B,求 ,求
,求 .
. 中,
中, ,则
,则
 B.
B. C.
C. D.
D.
 中,
中, , 则
, 则 。
。 内一点
内一点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则当
,则当 最小时
最小时 的值为( )
的值为( ) (B)
(B) (C)
(C) (D)
(D)
 ,
, 以及
以及 所围成的图形的面积等于( )
所围成的图形的面积等于( ) C.
C. D.
D.