题目内容
(本小题满分14分)已知函数 (
( ).
).
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)是否存在常数 ,使得
,使得 ,
, 恒成立?若存在,求常数
恒成立?若存在,求常数 的值或取值范围;若不存在,请说明理由.
的值或取值范围;若不存在,请说明理由.
(1) (2)存在
(2)存在 ,
, ,
, 恒成立
恒成立
【解析】
试题分析:(1)求导,得到曲线 在点
在点 处的切线斜率,代入点斜式即可;
处的切线斜率,代入点斜式即可;
(2)构造函数 ,
, 讨论其单调性可知,
讨论其单调性可知, ,
, ;
; ,
, 由由
由由 ,当
,当 时,
时, ,
, 的取值范围为
的取值范围为 ,当
,当 时,
时, ,
, 的取值范围为
的取值范围为
∵ ,
, 恒成立,∴
恒成立,∴
试题解析:(1) ,所求切线的斜率
,所求切线的斜率
所求切线方程为
即
(2)由 ,作函数
,作函数 ,其中
,其中

|
|
|
|
|
| - | - | 0 | + |
| ↘ | ↘ | 极小值 | ↗ |
由上表可知, ,
, ;
; ,
,
由 ,当
,当 时,
时, ,
, 的取值范围为
的取值范围为 ,当
,当 时,
时, ,
, 的取值范围为
的取值范围为
∵ ,
, 恒成立,∴
恒成立,∴
考点:曲线的切线方程,由导数研究函数的性质

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目







 ,则
,则 =________________.
=________________. 次射箭的环数依次是
次射箭的环数依次是 ,则该组数据的方差是 .
,则该组数据的方差是 . 中,设直线
中,设直线 与圆
与圆 交于
交于 两点,
两点, 为坐标原点,若圆上一点
为坐标原点,若圆上一点 满足
满足 ,则
,则 .
. 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则
的焦点重合,则 .
. ,
,  ,且
,且 .
. 的值;
的值; ,
, 是第二象限角,求
是第二象限角,求 .
.
 B.
B. C.
C. D.
D.
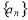 满足
满足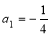 ,
,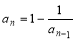 (
( ),计算并观察数列
),计算并观察数列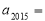 .
.  ,若
,若 ,则实数
,则实数 = .
= .