题目内容
已知数列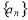
满足
，
（
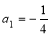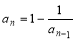），计算并观察数列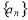的前若干项，根据前若干项的变化规律推测，
．
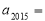【解析】
试题分析：由题意
，
，即数列
是以
为周期的周期数列，则
考点：数列的周期
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
优百分课时互动系列答案开心蛙状元作业系列答案题目内容
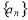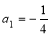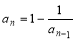已知数列满足，（），计算并观察数列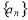的前若干项，根据前若干项的变化规律推测， ．
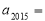【解析】
试题分析：由题意，，即数列是以为周期的周期数列，则
考点：数列的周期
优百分课时互动系列答案开心蛙状元作业系列答案
中，设锐角
的始边与
轴的非负半轴重合，终边与单位圆交于点
，将射线
绕坐标原点
按逆时针方向旋转
后与单位圆交于点
. 记
.
的值域；
的角
所对的边分别为
，若
，且
，
，求
.
（
）．
在点
处的切线方程；
，使得
，
恒成立？若存在，求常数
的离心率
B．
C．
D．
PB；
，若
存在唯一的零点
，且
，则常数
的取值范围是
B．
C．
D．
为实数集，
，
，则
B．
C．
D．
；条件q：直线y= kx+2与圆x2+y2=1相切，则p是q的（ ）
B．
D．