题目内容
【题目】过抛物线x2=4y的焦点F作直线AB，CD与抛物线交于A，B，C，D四点，且AB⊥CD，则 
+ 
的最大值等于 ．
【答案】-16
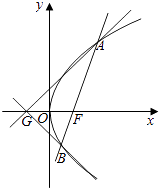
【解析】解：如图所示，
由抛物线x2=4y可得焦点F（0，1）．
设直线AB的方程为：y=kx+1，（k≠0）．
∵AB⊥CD，可得直线CD的方程为y=﹣ 
x+1．
设A（x1 ， y1），B（x2 ， y2），C（x3 ， y3），D（x4 ， y4）．
联立 
，化为x2﹣4kx﹣4=0，
得x1+x2=4k，x1x2=﹣4．
同理可得x3+x4=﹣ 
，x3x4=﹣4．
∴ 
=（x1 ， y1﹣1）（x2 ， y2﹣1）=x1x2+（y1﹣1）（y2﹣1）=（1+k2）x1x2=﹣4（1+k2）．
同理可得 
=﹣4（1+ 
）．
∴ + =﹣4（2+k2+ ）≤﹣4（2+2 
）=﹣16，当且仅当k=±1时取等号．
∴ + 的最大值等于﹣16．
所以答案是：﹣16．
练习册系列答案
相关题目
