Question

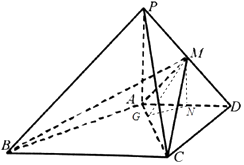
【题目】如图，在四棱锥中P﹣ABCD，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD=CD=2 ，BC=4 ，PA=2．
（1）求证：AB⊥PC；
（2）在线段PD上，是否存在一点M，使得二面角M﹣AC﹣D的大小为45°，如果存在，求BM与平面MAC所成角的正弦值，如果不存在，请说明理由．

Answer 1

【答案】
（1）证明：∵四边形ABCD是直角梯形，

AD=CD=2 ，BC=4 ，

∴AC=4，AB= = =4，

∴△ABC是等腰直角三角形，即AB⊥AC，

∵PA⊥平面ABCD，AB平面ABCD，

∴PA⊥AB，

∴AB⊥平面PAC，又PC平面PAC，

∴AB⊥PC

（2）解：假设存在符合条件的点M，过点M作MN⊥AD于N，则MN∥PA，

∴MN⊥平面ABCD，∴MN⊥AC．

过点M作MG⊥AC于G，连接NG，则AC⊥平面MNG，

∴AC⊥NG，即∠MGN是二面角M﹣AC﹣D的平面角．

若∠MGN=45°，则NG=MN，又AN= NG= MN，

∴MN=1，即M是线段PD的中点．

∴存在点M使得二面角M﹣AC﹣D的大小为45°．

在三棱锥M﹣ABC中，VM﹣ABC= S△ABCMN= = ，

设点B到平面MAC的距离是h，则VB﹣MAC= ，

∵MG= MN= ，∴S△MAC= = =2 ，

∴ = ，解得h=2 ．

在△ABN中，AB=4，AN= ，∠BAN=135°，∴BN= = ，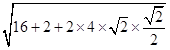

∴BM= =3 ，

∴BM与平面MAC所成角的正弦值为 = ．

【解析】（1）利用直角梯形的性质求出AB，AC的长，根据勾股定理的逆定理得出AB⊥AC，由PA⊥平面ABCD得出AB⊥PA，故AB⊥平面PAC，于是AB⊥PC；（2）假设存在点M，做出二面角的平面角，根据勾股定理求出M到平面ABCD的距离从而确定M的位置，利用棱锥的体积求出B到平面MAC的距离h，根据勾股定理计算BM，则 即为所求角的正弦值．
【考点精析】本题主要考查了直线与平面垂直的性质和空间角的异面直线所成的角的相关知识点，需要掌握垂直于同一个平面的两条直线平行；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则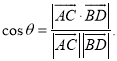才能正确解答此题．