题目内容
【题目】已知在平面直角坐标系xOy中,过点P(1,0)的直线l的参数方程是  (t是参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C点的极坐标方程为ρ=﹣4sin(θ﹣
(t是参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C点的极坐标方程为ρ=﹣4sin(θ﹣ ![]() ).
).
(1)判断直线l与曲线C的位置关系;
(2)若直线l与曲线C交于两点A、B,求|PA||PB|的值.
【答案】
(1)解:直线l的参数方程是 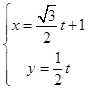 (t是参数),消去参数t可得普通方程:x﹣
(t是参数),消去参数t可得普通方程:x﹣ ![]() y﹣1=0.
y﹣1=0.
曲线C点的极坐标方程为ρ=﹣4sin(θ﹣ ![]() ),即ρ2=﹣4ρsin(θ﹣
),即ρ2=﹣4ρsin(θ﹣ ![]() ),可得直角坐标方程:x2+y2+4×
),可得直角坐标方程:x2+y2+4× 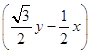 =0,
=0,
配方为(x﹣1)2+ ![]() =4,可得圆心C(1,﹣
=4,可得圆心C(1,﹣ ![]() ),半径r=2.
),半径r=2.
圆心到直线l的距离d= 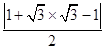 =
= ![]() <2=r.
<2=r.
∴直线l与曲线C的位置关系是相交
(2)解:把直线l的参数方程 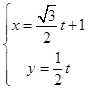 (t是参数),代入圆C的方程可得:t2+
(t是参数),代入圆C的方程可得:t2+ ![]() t﹣1=0.
t﹣1=0.
∴t1t2=﹣1.
∴|PA||PB|=|t1t2|=1
【解析】(1)直线l的参数方程是 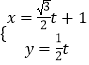 (t是参数),消去参数t可得普通方程.曲线C点的极坐标方程为ρ=﹣4sin(θ﹣
(t是参数),消去参数t可得普通方程.曲线C点的极坐标方程为ρ=﹣4sin(θ﹣ ![]() ),即ρ2=﹣4ρsin(θ﹣
),即ρ2=﹣4ρsin(θ﹣ ![]() ),利用互化公式可得直角坐标方程.求出圆心到直线l的距离d,与半径r比较可得直线l与曲线C的位置关系.(2)把直线l的参数方程
),利用互化公式可得直角坐标方程.求出圆心到直线l的距离d,与半径r比较可得直线l与曲线C的位置关系.(2)把直线l的参数方程 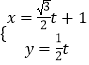 (t是参数),代入圆C的方程可得:t2+
(t是参数),代入圆C的方程可得:t2+ ![]() t﹣1=0.可得|PA||PB|=|t1t2|.
t﹣1=0.可得|PA||PB|=|t1t2|.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
用电量(万度) | 38 | 35 | 41 | 36 | 30 |
![]() xiyi=5446,
xiyi=5446, ![]() xi2=4538,
xi2=4538, ![]() =
= 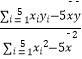 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.